Introduction

Computers and computation

There are several ways in which a machine can perform computations, each characterized by the primary effect it exploits:

• Mechanical
• Electrical
• Biological
• Optical

In addition to its physical implementation, a computational machine is described by the theoretical model of computation that governs it. some models are reported below:

Turing machine

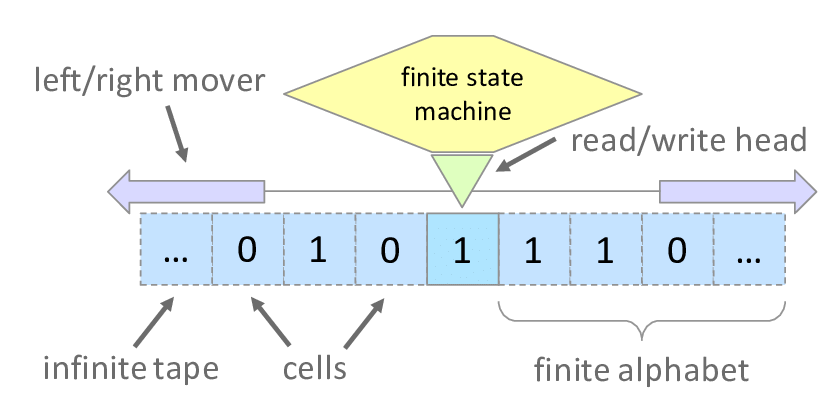
The Turing machine consists of:

1. Tape: Divided into cells that can hold symbols (such as 0 or 1) or remain blank. The tape is infinite in both directions.
2. Head: Positioned over a specific tape cell at any given time. The head can read the symbol on the current cell, write a new symbol, and move left or right along the tape.
3. State Register: Represents the internal state of the machine, determining its future actions based on the current state and the symbol read from the tape.

The machine operates through a set of rules or instructions that dictate its behavior. These rules define what action to take (read, write, move) based on the combination of the current state and the symbol being read.

The Church-Turing thesis proves that any function computable by an algorithm can be computed by a Turing machine. This means that if you can express a problem or algorithm in a systematic and step-by-step manner, a Turing machine can simulate it.

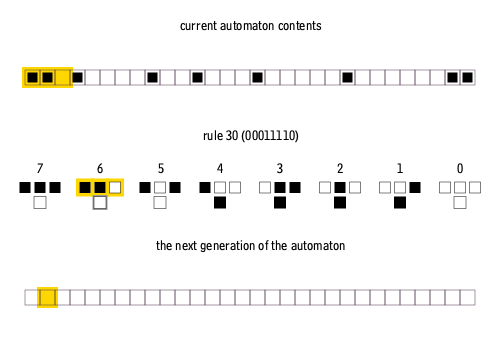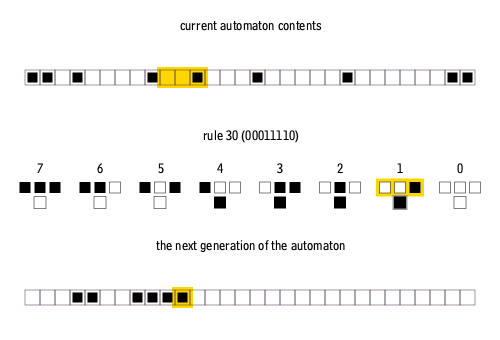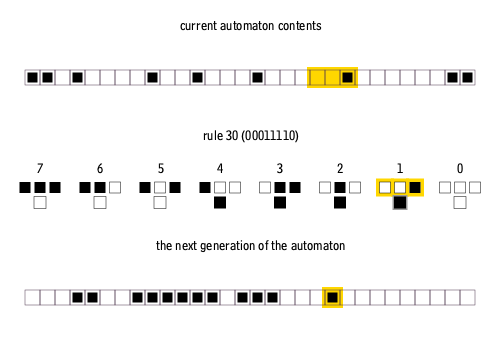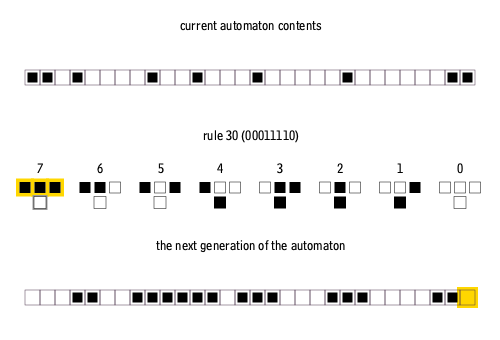
Cellular automata

Source

Cellular automata is a computational model defined by a grid of cells, each in a specific state. Rules determine how a cell’s state evolves based on its current state and the states of neighboring cells. The system evolves in discrete time steps, showcasing emergent complexity from simple local rules.

further info: Conway’s Game of Life

Von Neumann architecture

The Von Neumann architecture is a computer architecture model that consists of:

1. Memory: Stores both data and instructions, allowing for the storage and retrieval of information.
2. Arithmetic and Logic Unit (ALU): Performs mathematical and logical operations on data.

One distinguishing feature of Von Neumann architecture is that both data and instructions are stored in the same memory space, allowing programs to be easily modified and facilitating the development of more flexible and general-purpose computers. This architecture forms the basis for most modern computer systems.

Logic in memory architecture

Logic in memory architectures aim to address some of the limitations of traditional Von Neumann architectures, particularly the bottleneck created by the separation of memory and processing units. This model is being explored for its potential to improve performance in specific types of computations, such as those prevalent in artificial intelligence and data-intensive tasks.

Data representation

In classical computers data is represented by bits; bits represent a single -bit state. To implement parallelism we either need more hardware: have multiple CPUs that perform multiple operations in parallel, or to reuse the same hardware but in this case we need more time.

In quantum computers, on the other hand, with qubits we can represent components in one state.

Logic gates

In classical computers (where we use Boolean logic), single and two bit gates (such as NOT + AND) can be use to describe any Boolean function. The NAND and NOR gates are instead universal gates. In practice NAND and NOR gates are economical and easier to fabricate respect to other gates and they are the basic gates used in all IC digital logic families.

We can distinguish between single gates, which have only one input, and two gates, which have two inputs (but only one output).

Examples of single gate are the classical NOT gate

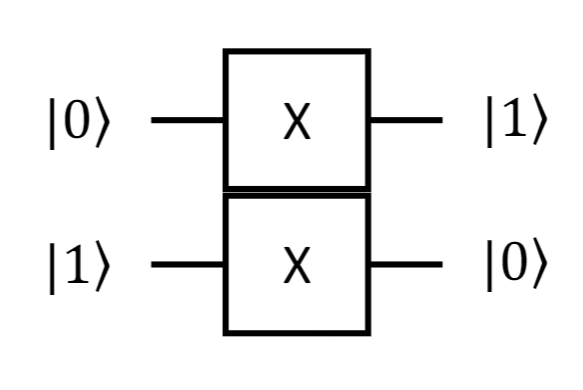
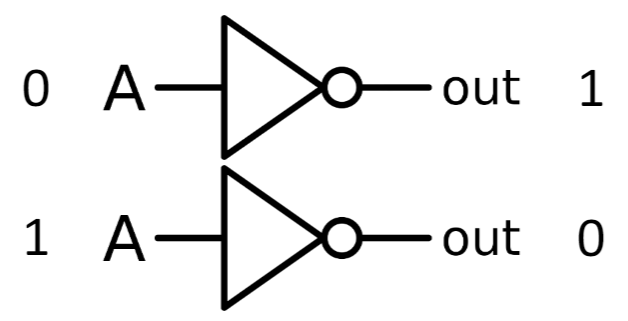and its quantum counterpart, the X-gate (which will be described in more details later)

Examples of two gates are the classical XOR-gate

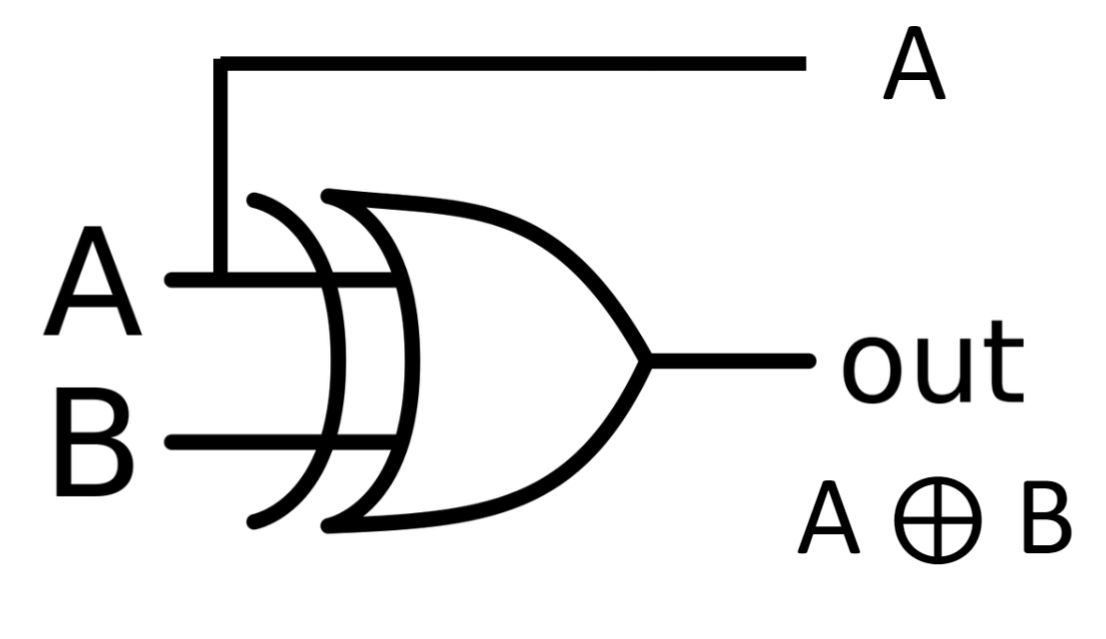which, if we consider the A bit as a control bit, can be seen as a “controllable NOT”:

The quantum counterpart is the CNOT-gate

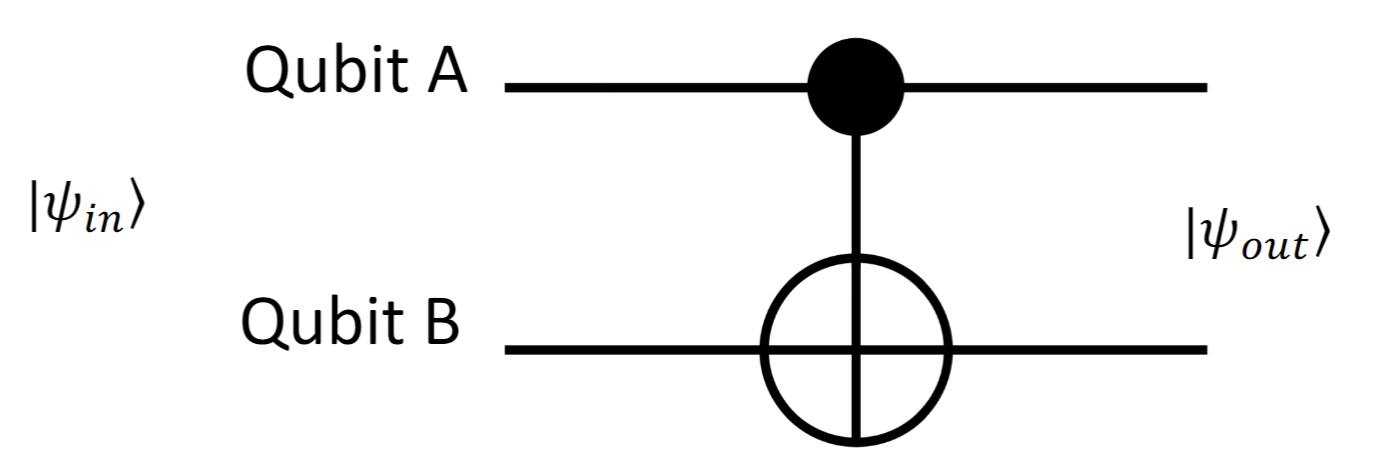
DiVincenzo criteria

When in the past people had to find a device which could implement a good logic element, they where searching for something that could satisfy the following criteria:

• Scalable in order to develop complex systems
• Easy to characterize and to manufacture in large scale
• Able to represent the information (bit)
• Easy to initialize in a wanted state
• Measurable in order to identify the state
• Robust against failure

The currently used device (the MOSFET) can satisfy all these criteria.

To make a good qubit, we need all of the above properties, plus:

• The ability to interconvert stationary and flying qubits (which are needed for communication)
• The ability to faithfully transmit flying qubits between specified locations

Qubit figures of merit

To understand if a qubit is a good qubit we can analyze the following properties:

Robustness

This property can be also represented by the coherence time, which is the amount of time before the quantum information is lost. It is mainly do to the interaction of the qubit with the environment.

There are two ways the qubit looses information: energy relaxation and dephasing, which will be studied more in detail in the following lectures.

Gate speed

In this category we have the gate time, which is the time required to perform an operation, and the number of operations that can be performed in the qubit lifetime. If the gate operations take longer than the coherence time, it increases the likelihood of errors due to decoherence

Gate fidelity

Finally we have the gate fidelity, which is a measure of how close the operations on the qubit are to the ideal case.

Qubits

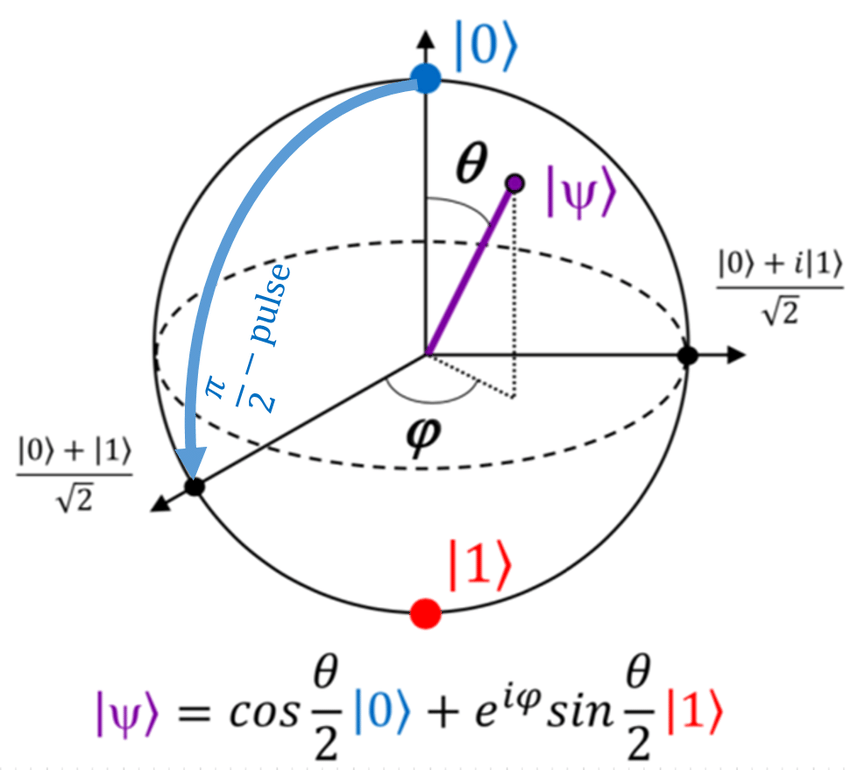
The Bloch sphere is a geometrical representation of the qubit state.

In general, a qubit can be represented as the superposition of two states denoted as and :

where and are complex numbers such that

Since measurements of quantum objects are projective measurements i.e. measuring the state of a qubit the state will collapse in either or . This implies that only one bit of information can be extracted from the qubit.

Since and are eigenstate of the operator we call this Z-measurement.

In general there is an infinite number of basis but the other common ones are

which correspond to the eigenstates of and .

Bloch sphere

On this topic you can also see the Condensed Matter lecture about qubits

The state of the qubit can also be written as

which can also be seen as the representation of a point on a sphere of radius (if the radius is different from then the wave function will not be normalized).

(Beckers, Arnout & Tajalli, Armin & Sallese, Jean-Michel. (2019). A Review on Quantum Computing: Qubits, Cryogenic Electronics and Cryogenic MOSFET Physics.)

Gates

All the gifs in this chapter are taken from here

Pauli gates

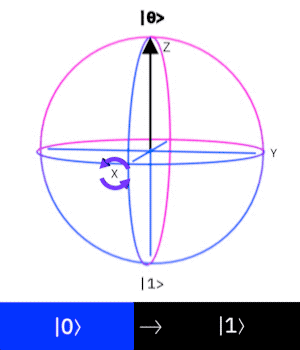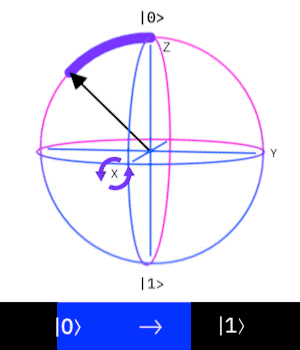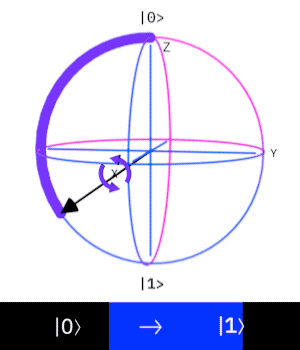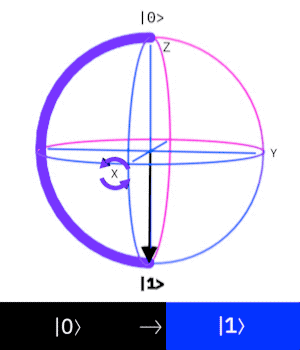
X-gate

The Pauli X-gate corresponds to a rotation around the x-axis by .

If we apply the gate to the state we get the following result:

Z-gate

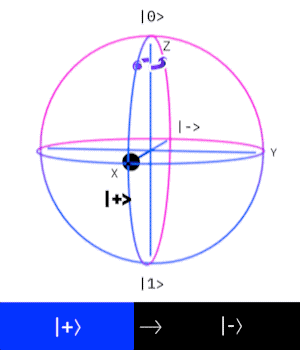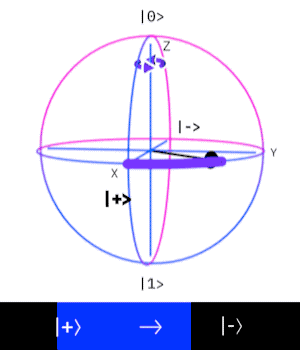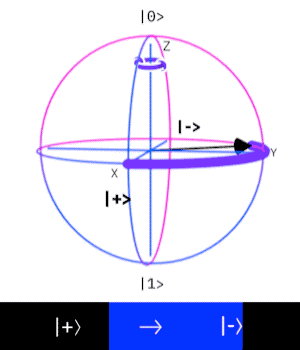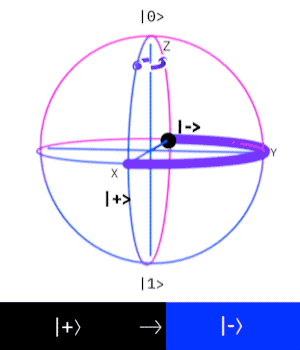
The Pauli Z-gate corresponds to a rotation around the z-axis by .

Y-gate

The Pauli Y-gate corresponds to a rotation around the y-axis by .

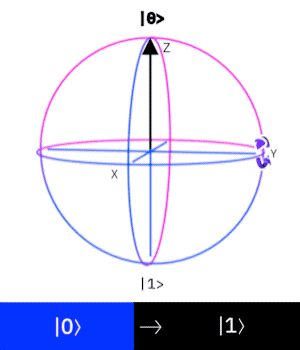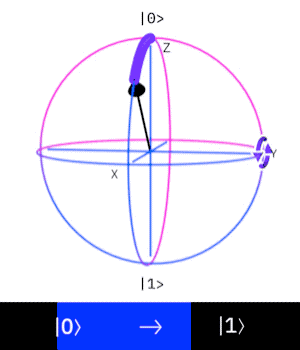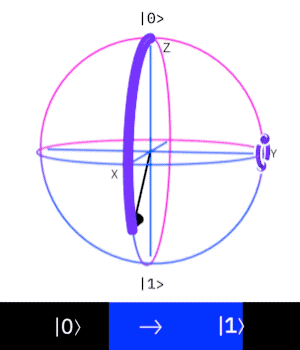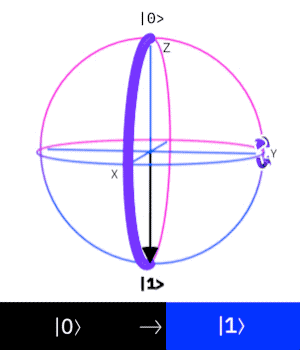
Properties of Pauli matrices

• Commutation relations :

• Anticommutation relations :

• All Pauli matrices are Hermitian, indicating that they are equivalent to their own conjugate transpose. Consequently, they possess real eigenvalues, exhibit orthogonal eigenvectors, and are observable in quantum mechanics.

Rotation gates

While Pauli gates can only rotate the state by , we can achieve an arbitrary rotation around the axis using the Pauli matrices using the following formula:

When the rotation angle is , the rotation operators implement the same operation as the Pauli matrices

Hadamard gate

The Hadamard gate is important because it allows us to bring the qubit into superposition (open the superposition).

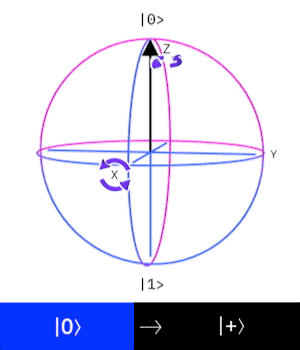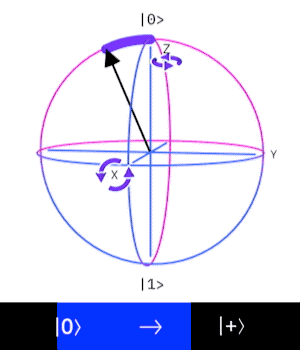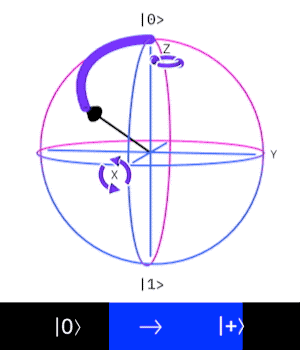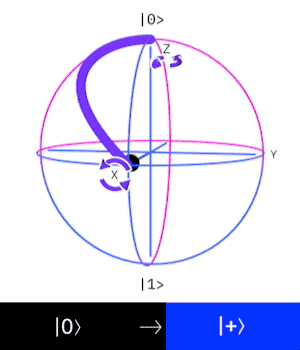
the Hadamard transforms a deterministic computational state into a superposition.

Phase gate

The phase gate, also known as the S-gate introduces a phase shift in the qubit without changing the basis states. In practice it adds to the phase of :

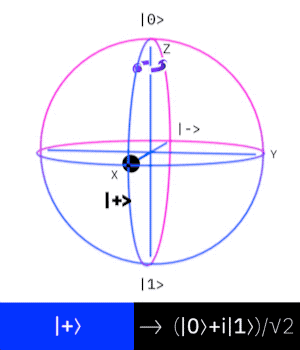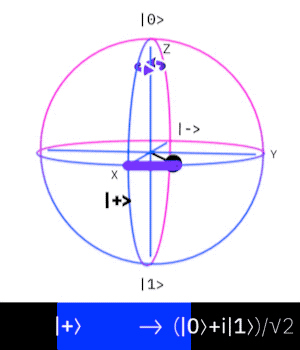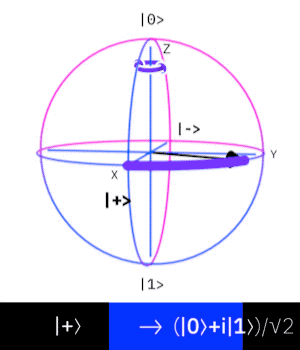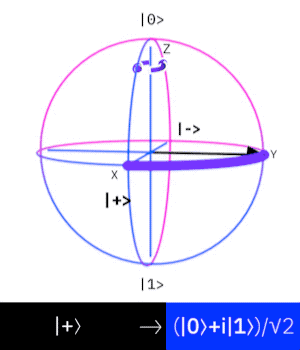
Density matrix

The formalism of unitary evolution for a quantum system assumes that the system under study is perfectly isolated from other quantum or classical objects and subject to error-free control. However, no physical system can be perfectly isolated, and the system will always be in contact with the NOISY classical WORLD.

It is therefore safe to say that experiments never prepare pure states (e.g. the ground state |0> in which the system is initialized); indeed, real quantum systems must be described using an ensemble operator, also known as the DENSITY MATRIX   (MIXED STATES).

The density matrix is a tool that allows us to take into account the fact that real systems are not pure states due to noise and to the interaction with the environment. The density matrix provides a way to represent both mixed and pure states.

For a pure state the density matrix is .

Some relevant properties of the density matrix are that:

• It must be Hermitian:
• Its trace (sum of the diagonal elements) must be normalized:

Example 2 level system

Density matrices are particularly simple in the case of two-level systems. If the qubit is a pure state , the density matrix would be

• The elements on the diagonal represent the probabilities of finding the system in the states and respectively.
• The off-diagonal elements represent the quantum correlations between the states and .

in general

to ensure that the density matrix is Hermitian, the off-diagonal elements must satisfy .

Absolutely, I can replace the formulas in the text with LaTeX code:

It is important to emphasize the difference between a probabilistic mixture of quantum states and their superposition. If a physical system is prepared to be either in state or , with equal probability, it can be described by the mixed state

where and are assumed orthogonal. On the other hand, a quantum superposition of these two states with equal probability amplitudes results in the pure state ​ with density matrix:

Unlike the probabilistic mixture, this superposition can display quantum interference.

To better understand the difference between pure and mixed state we recommend: https://www.youtube.com/watch?v=LR5kfhrs4Cc