Crystals
Types of solids
Monocrystal Polycristal Amorphous In a monocrystal all the atoms are arranged on a common lattice structure, in a polycrystal there are multiple lattices of the same type oriented differently to one another (each lattice is called grain), the interface between two grain is called Grain boundary. In amorphous material, on the other hand, the atoms are placed randomly in space.
While we will analyse mostly monocrystals, it is important to note that all three types are useful in practical applications, such as the creation of integrated devices.
Link to original
Bravais lattice
A Bravais lattice can be defined in two ways. The informal definition states that a lattice is a Bravais lattice if any point is equivalent to any other in terms of symmetry and relations to the other point (i.e. if I am on a point and then move to another point I cannot tell the difference).
The mathematical definition instead is as follows
Primitive unit cell
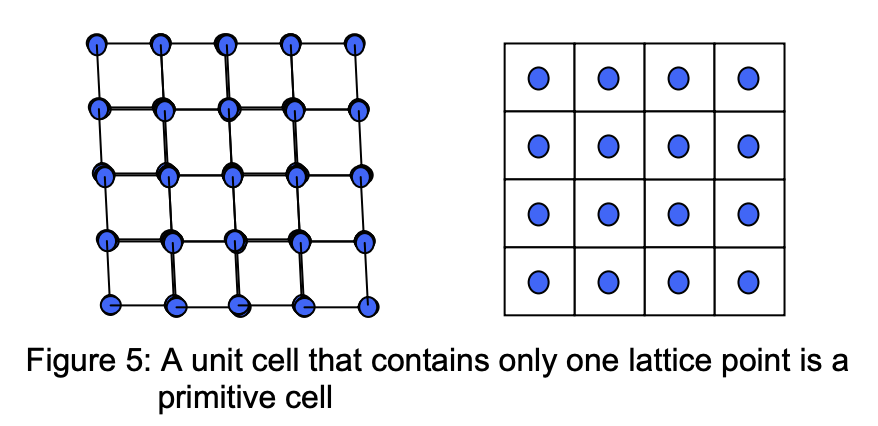
A primitive cell unit is defined as any volume of space which, when translated through all the vectors of the Bravais lattice, fills the space without overlap and without leaving voids.
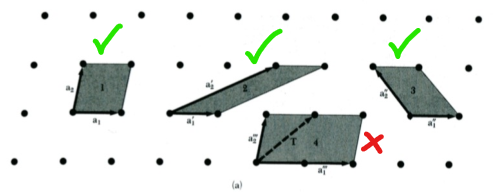
A primitive cell always contains one lattice point only; if the point is on the edge of the cell only a fraction of it is considered (if a point is shared between 4 cells, each cell will have 1/4 of it). The basis associated with a primitive cell is called a primitive basis.
Conventional unit cell
It is often used to describe the periodicity of crystals; such as in cases where the unitary primitive cell is not the most convenient way to describe the crystal’s geometric structure. Such a cell contains more than one primitive lattice point.
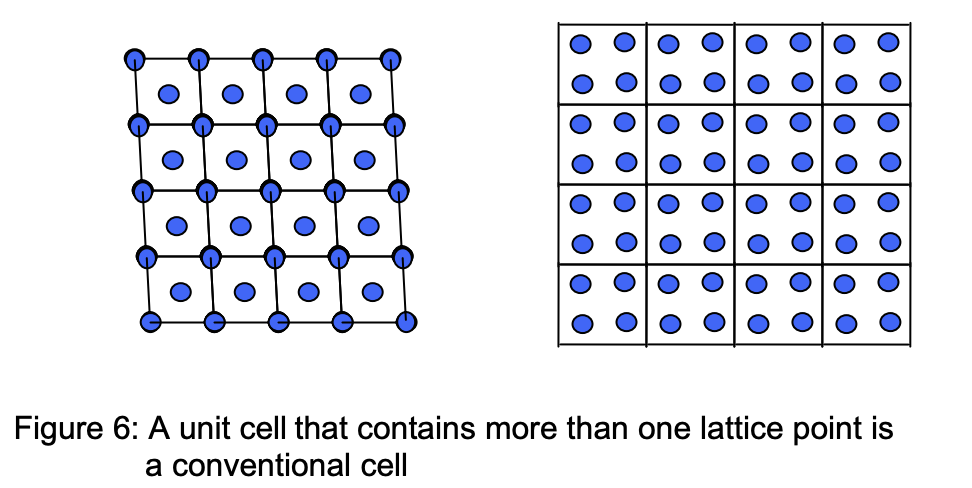
An example is the body-centred cubic (bcc) lattices that are described in terms of a cubic unit cell. Where the conventional unit cell of bcc is twice the primitive bcc unit cell.
Wigner-Seitz cell
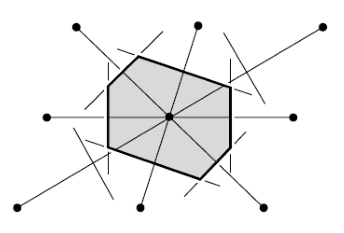
Wigner-Seitz cell is a special choice of primitive unit cell: region of points closer to a given lattice point than to any other.
How to draw it in 2D:
- Find the point for which you want to draw the cell.
- Draw lines that connect it to all its nearest neighbours.
- For each of these lines draw a perpendicular line(
) that passes through its mid point. - The area delimited by the lines (
) is the Wigner-Seitz cell.
Bravais lattice
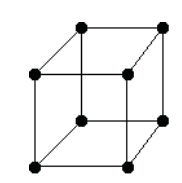
There are only 14 unique lattices possible in 3 dimensions called Bravais lattice. We are mostly interested in studying the cubic lattice which comes in three forms:
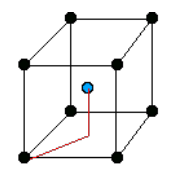
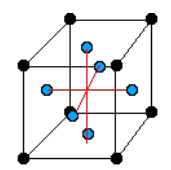
Simple Cubic Body Centered Cubic (BCC) Face Centered Cubic (FCC) the blue atom is in the center of the cube the blue atoms are on the faces of the main cube Each lattice has a specific lattice parameter
Link to originalwhich represents the length of the cube side.
It should be noted that BCC and FCC are not primitive because they contain more than one point (the primitive cell wouldn’t show the cubic symmetry).
Crystal structure
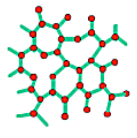
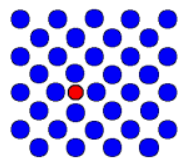
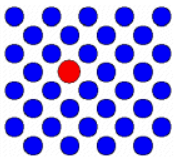
Bravais lattice is an abstract concept which is useful to characterize a crystal. The crystal itself is made out of a Bravais lattice and a basis. The basis can be one atom or a molecule.
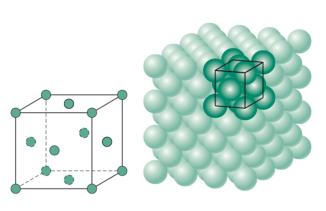
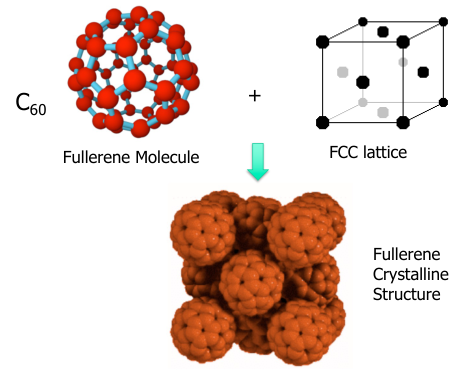
In the images above we can see that the unit of repetition (the basis) is an atom in the first case and a molecule in the second, but the lattice is the same. Changing the basis changes the coordination number which is the number of atoms connected to a specific atom.
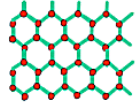
Silicon crystal structure
![]()
In the image above it is possible to see that the unit of repetition in this case is made of the two red atoms and that the coordination number is 4. The atoms positions in the primitive cell are expressed in fractional coordinates which means that they are expressed as a fraction of the lattice parameter a.
Reciprocal lattice
The reciprocal lattice originates from mathematical transformations applied to the Bravais lattice. This process is crucial because it allows us to delve into reciprocal space, where we gain a clearer and more insightful understanding of various physical properties inherent to crystals.
Let’s start with a Bravais lattice
We define the reciprocal lattice
note that the number of
We need to find a base for
where
Since we can find
which is again a Bravais lattice.
Example in 2D
We can calculate the base vectors of the reciprocal space using the constraints given above.
We can then draw the Wigner-Seitz cells for the two lattices. The WS cell of the reciprocal space is called Brillouin zone. (the choice of WS is not mandatory, it is just practical in this example)
Example: electrostatic potential
The electrostatic potential in a crystal is periodic:
We will use the generic function
Defects in crystalline solids
We are interested in studying defects in crystals because some of them (point defects in particular) are used in quantum engineering to achieve desired results. Doping for example is a kind of point defect.
Non ionic crystals defects
In the following table it is possible to see some kinds of point defects that can affect non ionic crystals (crystals made of one type of atom only).
Point defects
Link to original
Type Explanation Image Self interstitial There is an extra atom of the right element Interstitial There is an extra atom of the wrong element Vacancy An atom is missing Substitutional impurity There is a wrong atom in the right place of the lattice
Ionic crystals defects
In ionic crystal (made of two kinds of atoms, one positive ion and one negative), there are two common defects.
| Schottky | Frenkel |
|---|---|
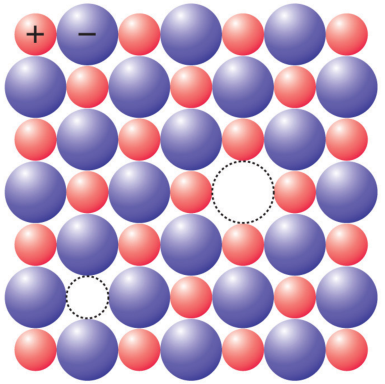 | 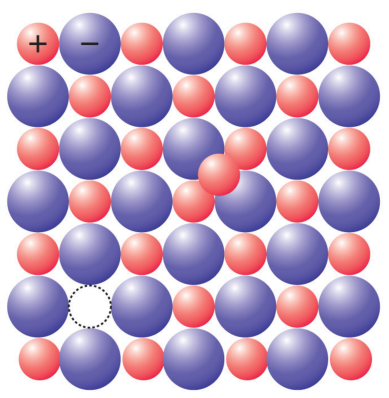 |
The Schottky defects correspond to a missing cation/anion pair while Frenkel defects correspond to a vacancy and a nearby interstitial of the same ion.
Defects formation energy
We would expect no defects at thermodynamic equilibrium but this is not the case because forming defects increases the entropy which stabilizes the system (?).
Pairs of point defects
In ionic crystals the charge is carried not by electrons, but by the ions themselves; this would be extremely difficult to achieve in a perfect crystal but can happen easily in the presence of vacancies which can allow the motion of units of positive charge.

Color centers
Alkali-alide crystals are transparent throughout the visible region of the spectrum. But may become coloured in presence of defects.