Reciprocal lattice

Let’s start from studying the simple case of a 1D crystal whose atoms are arranged in a line at a distance (period) from each other.

Let’s now introduce a function that has the same periodicity of the crystal:

If we write the Fourier expansion of we get

It is easy to show that due to the periodicity of , only some specific values of satisfy the relation above. In fact we have:

So if we have a periodic function its Fourier expansion can be written only for certain values of .

3D case

This can be generalized in 3 dimensions as follows:

with

Similarly to before, the Fourier series can be written as

with

Similarly to the demonstration above we can write

If

the last exponential becomes and we get:

Again, the sum is not on every possible wave vector.

Finding a base

It can be useful to define a base to express :

We now need to find that satisfy the condition for each .

If we take the particular case in which is parallel to :

we get

which (since is a generic integer) is true when

The same can be done for and getting the condition:

The vectors are the vectors of the reciprocal lattice and are the primitive vectors.

Dimensionally and thus the wave vector (for example) is perpendicular to and .

We can see that there is an inverse proportionality between the lengths of the vectors:

where is the angle between and .

Volume of the reciprocal lattice

Given the volume of the direct lattice we can find that the volume of the reciprocal lattice is

Theorem

Given the Miller indices we can prove that

and

where id the distance between adjacent planes.

Demonstration omitted

X-Ray diffraction

Bragg formulation

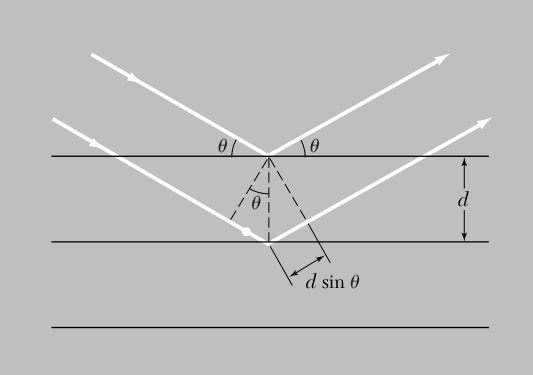
In the Bragg formulation the crystal is made by parallel planes and the constructive interference happens only for certain such that the difference in optical path is proportional to the wavelength. More precisely, given the difference in optical path (the extra distance) , we have constructive interference if

and thus

Von Laue formulation

In the Von Laue formulation we start by taking two lattice points (in red) and supposing that every atom can irradiate the incident radiation in every direction.

( and it has the same direction of ) (not sure)

We can say that the two wavelengths are equal

and that the two wave vectors are:

In this case the difference in optical path is

And the constructive interference happens when, like before, is an integer multiple of the wavelength:

So we get

Since the two lattice points are “connected” by we can also write the expression above as (todo is this true????)

which is the definition (?) of reciprocal lattice .

So the Von Laue condition can be written as

A different way to write the same formula, using the fact that is:

Equivalence of the formulations

To show that the two formulations are equivalent we can start from the second version of the Von Laue formulation ()