Nearly free electrons

Starting from the free electron model () we want to study what happens as the potential slowly increases (but remains weak).

Zero potential

Even for we need to consider the periodicity of the potential in order to be able to increase it later. The Bloch states are

but, since , and thus as expected for the free electrons.

This result has to be considered together with the fact that (due to the periodicity of the reciprocal lattice)

this implies that we have an infinite number of parabolas ( depends on ) shifted by .

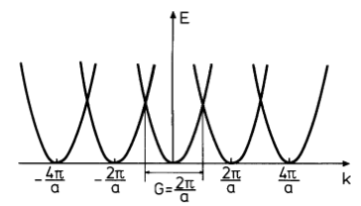
As we can see from the plot above, we can shift everything inside the first BZ to get what is called reduced zone scheme.

Potential different from zero

If we expect Bragg reflections associated with the Von Laue condition:

We know that Bragg reflection is a characteristic feature of wave propagation in crystals. Bragg reflection of electron waves in crystals is the cause of energy gaps. […] These energy gaps are of decisive significance in determining whether a solid is an insulator or a conductor. We explain physically the origin of energy gaps in the simple problem of a linear solid of lattice constant a.

Kittel, page 164

1D example

In case of a 1D crystal with spacing we get and the Von Laue condition becomes:

which means

For the first Bragg reflection () we can write as the linear combination of the two standing waves

todo WHYYYYYYYYYYYYYY?????????????

The standing waves are labelled or according to whether or not they change sign when is substituted for . Both standing waves are composed of equal parts of right- and left-directed traveling waves.

Kittel, page 165

Electronic density

Ibach Luth, 7.2

The two standing waves and pile up electrons at different regions, and therefore the two waves have different values of the potential energy in the field of the ions of the lattice. This is the origin of the energy gap.

Kittel, page 165

We have, in fact, that the electronic density is given by , which, for the two wavefunctions above, results in

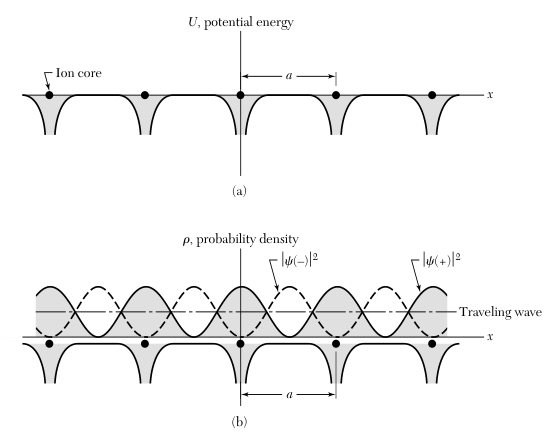
As we can see from the plot above, piles up electrons on lattice sites (i.e. where the ions are), thereby lowering the potential energy in comparison with the average potential energy seen by a traveling wave. , on the other hand, piles up electrons between the ions thereby raising the potential energy in comparison with that seen by a traveling wave.

Kittel, page 166

As we can see from the picture above, in the case of a 1D lattice with a weak potential, the energy is similar to the free electron case “far” from the lattice points (where the influence of the ion is weak and thus we are almost in the free electron case). Near the lattice point, on the other hand, the potential of the ions affects more the electrons with low (the electrons with low energy) and thus the parabola will be “squashed”, electrons with higher energy, on the other hand, will “care less” about the weak potential of the lattice and will behave almost as in the free case.

Quantitative description

Ibach Luth, 7.2

todo

Starting from the Schrödinger equation in k-space:

we want to estimate the coefficients

and a translation by a reciprocal lattice vector yields

considering :

is weak, so the eigenvalues are similar to those found for the free electron, this means that also the energy is nearly the free electron energy ().

We also make the assumption that only the largest are of interest, in fact we expect the greatest deviation from free electron behaviour when the denominator of the relation vanishes:

this is the Von Laue (Bragg) condition, the maximum perturbation occurs at the edge of the first Brillouin zone For this approximation we only need to consider two relations, one is the Bragg condition, the other is when and so we consider the .

Evaluating the coefficients in each condition we have:

1. Bragg:

the other terms are negligible, only and are “big” and significative.

the significant coefficient are again only and

Supposing , and putting together the two condition the system is:

this system has solutions if the determinant of the coefficients is zero

The potential is real, and its Fourier coefficients are:

and if the potential is real

and so .

Defining and

The determinant is:

at the edge of the first Brillouin zone,

and substituting in the energy relation above:

At the edge the contribution of the two waves with and re equal; the difference between the two energies at the boundary is equal to the band gap: