Landauer effect

Conductance

Formula for the conductance in a material

where is the cross-section is the length and is the material dependent conductivity.

Ballistic transport

Ballistic transport refers to the condition where electrons or other charge carriers move through a material without being scattered by impurities, defects, or lattice vibrations within that material. In typical conductive materials, electrons often collide with atoms and other electrons, which scatter them in different directions. This scattering limits the flow of current and contributes to electrical resistance. However, in ballistic transport, electrons can travel through the conductor (often a very thin or very clean wire, or a nanoscale device) at high speeds and over relatively long distances without scattering.

This happens when the dimensions of the material are shorter than the mean free path of the electrons, which is the average distance an electron travels between collisions.

Definition of mean free path:

where is the electron speed at Fermi level and is the average time between collisions.

Ideal quantum wire

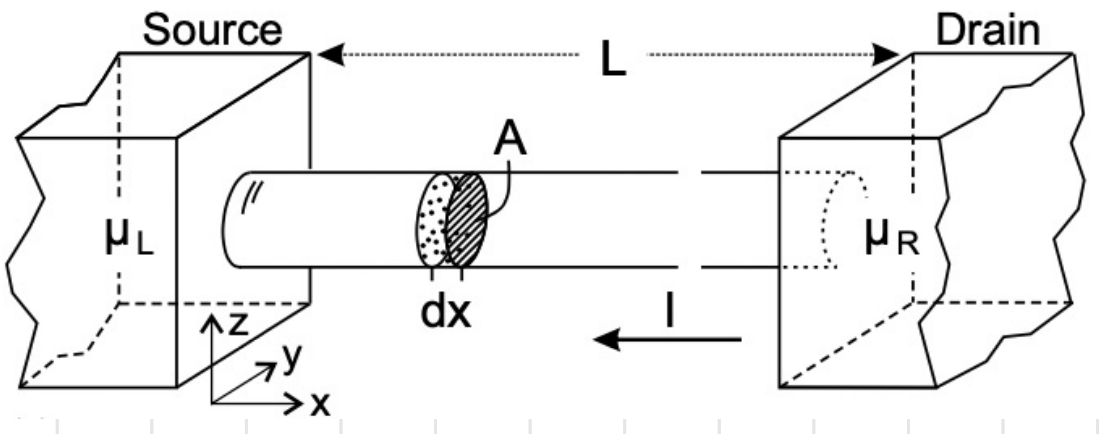
We make some assumptions to simplify the scenario and be able to arrive at the result:

• No scattering event, transport in the channel is perfectly ballistic
• The electrons entering the reservoir contacts are instantaneously in equilibrium with them.
• Contacts are reflectionless: the transmission probability from wire to contact is unitary
• Temperature=0
• The chemical potential of the left side its higher than the chemical potential of the right side so that electrons will flow to the right

Let’s see the solution of the Schrödinger equation for the wire, which we already know them from Quantum Wire:

Simplified case: single band

Now, recalling the definition of the current from the classical physics:

where the total charge in a small volume of length is :

so we can write:

The goal is to write the current as a function of the energy since it is what changes from left to right. The number of electrons in the wire is:

We can substitute this expression in the formula above to get the current as a function of the number of electrons:

We want to write the current as function of the energy. We take an infinitesimal of and write it as dependent on :

can be written as follows considering the definition of group velocity () and the relation :

We get

The last piece to get to the desired formula is . We can calculate it considering that the number of states allowed, , within a is given by their minimal spacing that is .

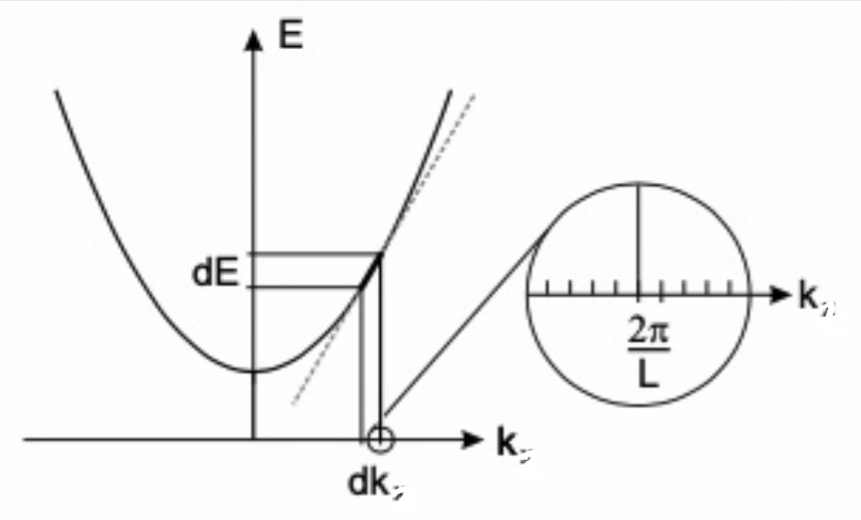
Taking into account also the spin degeneracy (which doubles the number of states), we get:

Substituting this expression in we get:

Finally, the total current can be calculated as the difference between left and right current:

Now that we have an expression for we can simply integrate it to get

The factor is called quantum of conductance.

In summary, we have shown that the conductance of a one-dimensional system with one occupied subband only depends on fundamental constants, namely the elementary charge and the Planck constant . Importantly, it does not depend on the dispersion relation or the Fermi energy .

Multiple bands

In this case the ideal wire is made of multiple bands, each band contributes to the current.

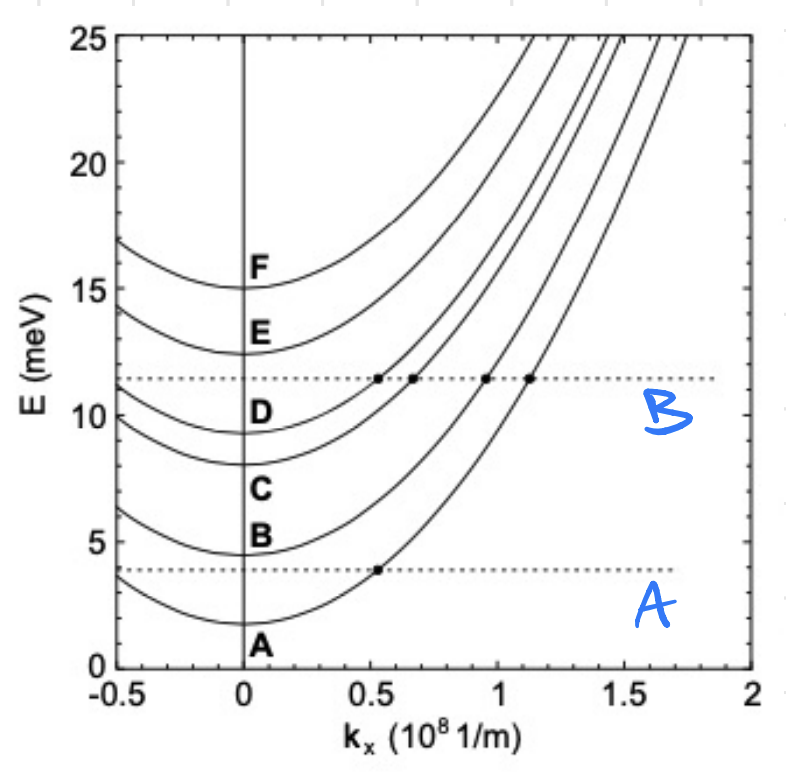
Situation A is the previous one while situation B is the general case.

To find the current energy relation in this case we need to make an approximation.

Linear response approximation

We need to prevent and to be on a different number of bands, thus we impose

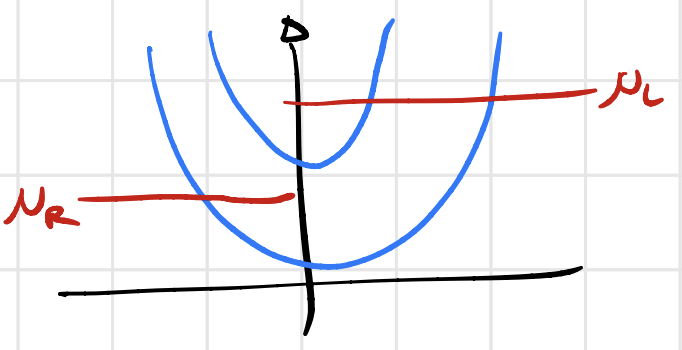
In this case the current is:

We define as the number of sub-bands crossed by

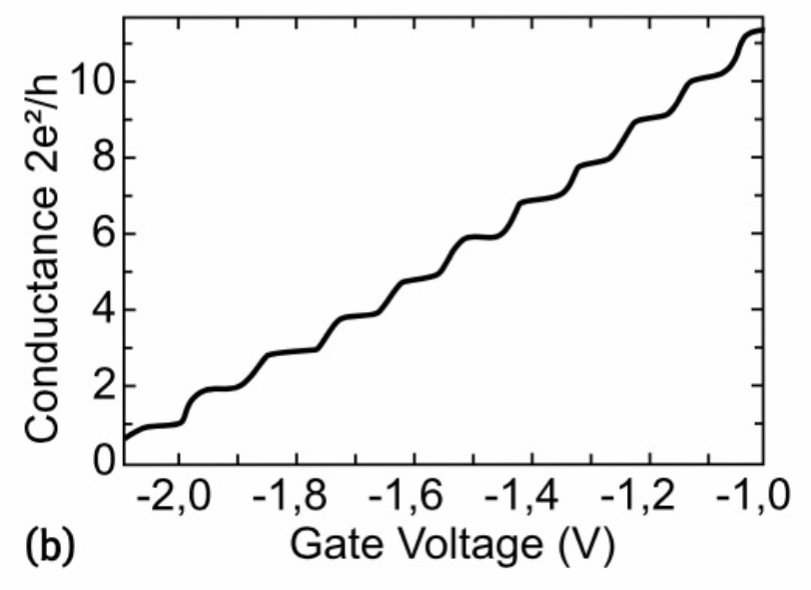
Since in real devices the electrodes are not ideal, the transmission coefficient is not unitary, and thus

depends on the the applied voltage and on the structure of the channel, it can be calculated only with simulations.