Thermal properties

Kittel, 5

In solids, the heat capacity is defined as

where is the energy of the system and is the temperature.

In a previous lecture we evaluated the contribution of the electrons to the heat capacity, getting that their contribution is minimal. What we want to do now is to calculate the contribution of the phonons to the heat capacity (); to do this we need to calculate the total energy of the phonons. This can be obtained as a summation of the energies over all the possible wave vectors and polarizations (todo when did we talk about polarization???).

where is the occupation probability at thermal equilibrium for phonons with wave vector and polarization .

follows a Bose Einstein distribution:

The shape of is reported below

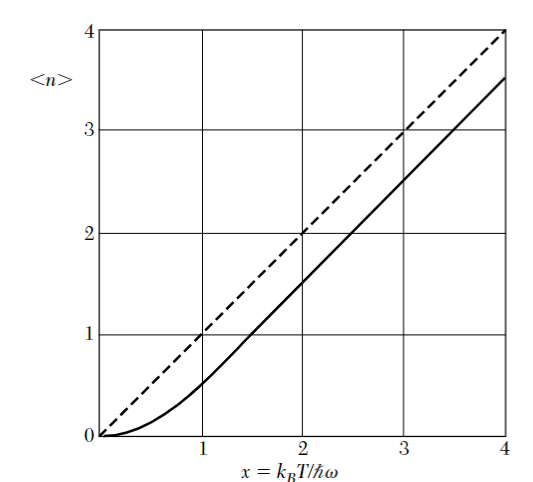
From equation we can transform the summation over in an integral by introducing the phononic density of states which represents the number of phononic states per unit frequency

this means that the number of states between and is given by (rearranging the formula above):

this consideration allows us to rewrite as

which can now be derived to obtain the heat capacity:

To further expand the integral we need to calculate .

Phononic density of states

todo

Debye model

My guess

to calculate Cv we still need to find the dispersion relation and thus we approximate it in different ways, one of which is the debye model?

In the Debye approximation we assume that the dispersion relation is linear:

where is the velocity of sound in the material and is assumed constant.

With these assumptions the DOS from above becomes

If we consider a monoatomic crystal with primitive cells, we expect to have 3 acoustic branches with independent states on every branchtodo explain.

We will have a maximum allowed frequency (cutoff frequency) called Debye frequencytodo why?

Its values can be obtained like thistodo what is this?

From this we can also get the maximum allowed wavelength:

We can now proceed to calculate the energy for a specific polarization

Supposing that all polarization have the same velocity (todo what does velocity have to do with this?) we get

If we define and we can rewrite the expression above as

is called Debye temperature:

Finding the heat capacity

We can finally derivate the total energy we just found to get the heat capacity:

In the second step above we used the fact that

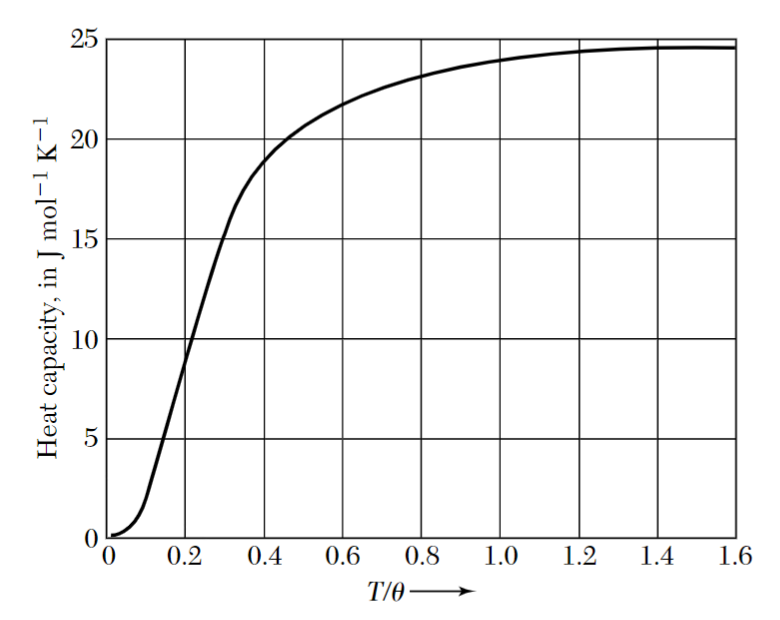
The plot above shows that the Debye heat capacity approaches a constant value equal to for .

Behaviour at low temperatures

In a previous lecture, we saw that the contribution to the heat capacity at low temperature given by electrons is proportional to and we anticipated that the phonons contribution is proportional to . We now want to prove this statement.

At very low temperatures () we can approximate with ( ). This means that we can recalculate the changing the upper limit in the integral to . Doing this we get that

(the calculation is omitted, the important thing is that the integral doesn’t depend on and thus doesn’t change the term).

This result can be interpreted in the following way:

At temperature , only the phonons with will be excited