Tunneling and T matrix

Transport Matrix

Davies, 5

A generalized “barrier” is any disturbance of an otherwise flat potential. We will start considering the step potential problem.

When an incoming electron approaches the potential barrier at position , its quantum wave interacts with the barrier. Similar to optical reflection indices for light waves, a portion of the electron’s wave is reflected, while another portion is transmitted into the barrier.

The wave functions for the two region are:

with:

The wavevector ​ is real, whereas the wavevector ​ can be either real or imaginary, depending on the relationship between and ​. Specifically, if ​, then the wavevector ​ is imaginary; otherwise it is real.

The continuity of the wavefunctions and of their first derivatives in implies:

so making the calculation we get that:

these are our two boundary conditions. We can write the amplitudes and as linear combination of and :

Since we can express and as linear combinations of and , we can apply a matrix formalism known as the T-MATRIX (Transport matrix). This allows us to write:

The matrix provides the amplitudes in region 2 based on the amplitudes in region 1. So in our case with one step potential we have that:

In general, , , , and are complex values, but for simplicity, we can set , , , and . This simplification makes our context easier to work with. We can designate as the reflection index and as the transmission index, as they represent the amplitudes of the reflected and transmitted components respectively.

solving the system we get:

the relation above always apply in the case of , , , and .

If instead of a barrier in we have a barrier in the Matrix T change as follow:

or

This approach can also be extended to subsequent regions and barriers. The power of the matrix formalism lies in the fact that the treatment becomes a straightforward multiplication of matrices.

also in the case of regions ( barriers) we have that if , , , and we have the following relations:

If our system is invariant with respect to time inversion and is symmetric with respect to the barriers, the transfer matrix’s determinant is equal to 1 so, in these cases

and we have that and .

We can write the total transmission probability as:

Quantum and classical transmittance

we can see that the quantum case differ from the classical one not only when but also when it is .

Some of the parameters that influence the transmittance index:

Height of the Barrier: The probability of tunneling decreases exponentially with the increase in the barrier’s height.

Width of the Barrier: The tunneling probability decreases exponentially as the width of the barrier increases.

Mass of the Particle: Heavier particles have a lower probability of tunneling compared to lighter ones.

Resonant-tunnelling diode

An interesting application of resonant tunneling is the RESONANT-TUNNELING DIODE which typically consists of a central layer of undoped GaAs separated from doped GaAs contact regions by means of (or ) tunnel barriers.

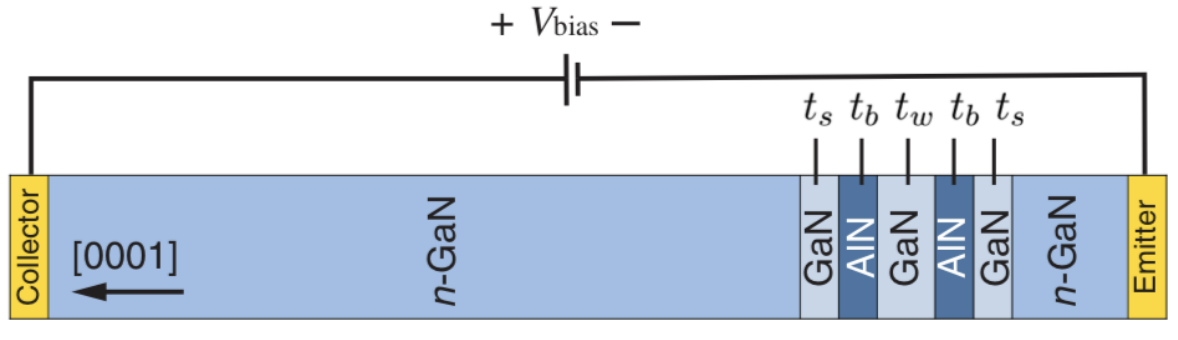
Resonant tunneling is induced by applying a variable voltage bias between the contacts which possibly matches the (first) resonant energy .

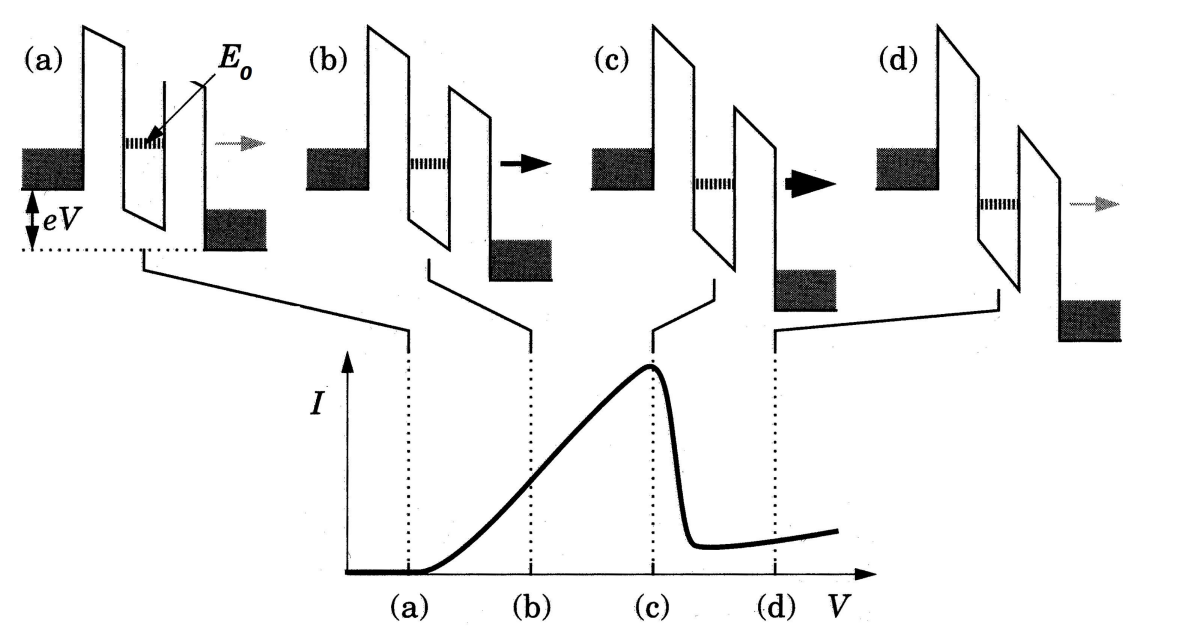
The image illustrates the operation of a resonant tunneling diode (RTD).

Section (a): Small Bias Applied

When a small voltage is applied across the device, the resonant level (the energy at which electrons can tunnel resonantly) is above the Fermi energy (the highest energy an electron has at absolute zero temperature) of the source contact. Because the resonant level is higher than the energy of most electrons, very few can tunnel through, resulting in a small current.

Section (b): Increased Bias

As the voltage (bias) increases, the resonant level aligns with the Fermi level of the source, allowing electrons to tunnel through the well more easily. The alignment of the resonant level with the Fermi energy increases the current sharply because many more electrons have the right energy to tunnel through the resonant level.

Section (c): Higher Bias

When the bias is increased further, the resonant level moves below the Fermi level of the source. This condition still allows a significant number of electrons to tunnel through, so the current remains high, but there is a decrease in the current.

Section (d): Too High Bias

At a very high bias, the resonant level drops too low, below the energy of most electrons in the source. This misalignment means that fewer electrons have the energy to tunnel through the barrier, and thus the current decreases rapidly.

Coulomb blockade

Is a phenomenon where the transfer of an electron to a small conducting island is prevented due to the repulsive force (Coulomb force) from electrons already present on the island. In essence, it becomes energetically expensive for additional electrons to join the island once a certain number of electrons are present, due to the increase in electrostatic energy. This phenomenon applies a more restrictive condition for the transmission of electrons from source to drain towards the barriers. Indeed even if an electron has the right energy (energy in the range align with the resonant energy), it still might not get through because of the repulsion from other electrons.

The increase in electrostatic energy of the system associated with the transfer of a charge in the island is:

When electrons have been transferred to the island, the change in electrostatic energy of the system is given by :

where we replaced with . So the increase of energy associated to the transfer of only one electron is given by:

we can notice that if the increase of energy associated to the transfer of only one electron is 0 and we have the resonant tunneling transport of electrons.

The Coulomb blockade prevents electrons from randomly moving onto the island due to thermal energy or electrical noise. It ensures that electron transfer only happens under very controlled conditions, the resonant condition.

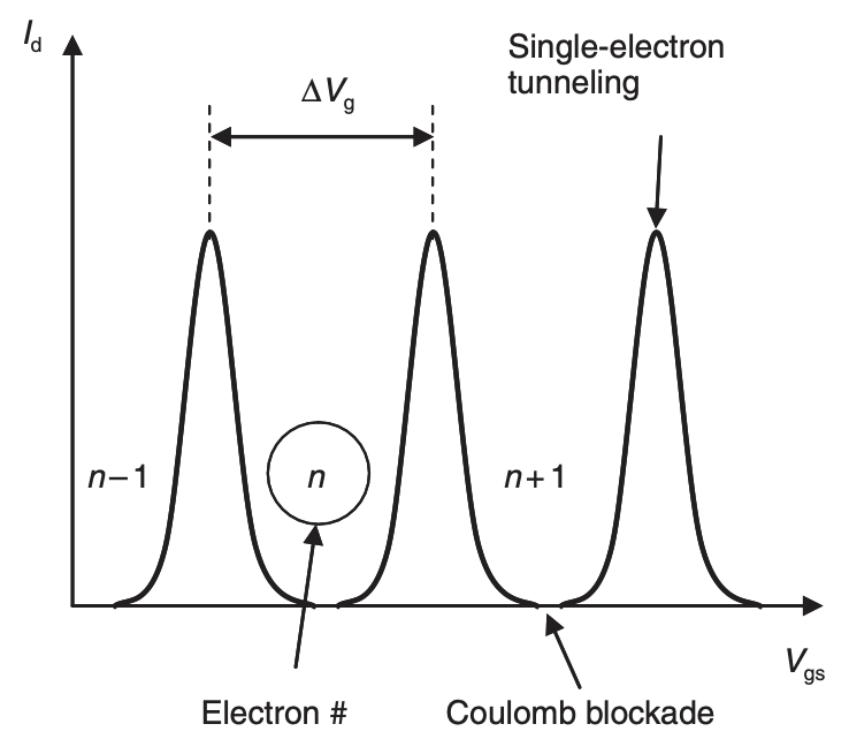
This phenomenon can be exploit to create a transistor device which can control the flow of individual electrons. That is the principles used in SET (Single-Electron Transistor)