Cryptography

Symmetric encryption

Terminology

• Message in clear: plain text or clear text, we will refer to it as P.
• Encrypted message: cyphertext, we will refer to it as C

Kerchoffs’ principle

If the keys are kept secret, managed only by trusted systems and of adequate length, then there is no need for the algorithm to be kept secret, it is better to make it public so that it can be studied and possible defects can be corrected.

If the Kerchoffs’ conditions are met, then the only possible attack is the brute force attack which requires a number of trial where is the number of bits of the key.

Symmetric cryptography

In symmetric cryptography there are two identical keys K which are share between sender and receiver (only!). The encryption consists in applying a mathematical function enc on the key-plain text pair C = enc(K, P), the decryption, on the other hand, uses a function dec = enc^-1 which, given the same pair as before, returns the plain text P = dec (K, P). Note that the key is always the first argument.

Symmetric cryptography has a low computational load but has a major flaw (which will be analysed later), which is how to securely share the key between sender and receiver.

XOR function

The XOR function is often used in cryptography because it is the ideal “confusion” operator (a random input will generate a random output). The XOR operates on two bits and the result is if the bits are identical, otherwise.

It is also very important to notice that the XOR is the inverse of itself .

DES

The DES (Double Encryption Standard) algorithm was one of the most used algorithms in the past decades (nowadays it is extremely easy to attack and should never be used). Its main advantage was its efficiency, since it used only three simple operations: XOR, shift and permutation. The first two are operation that can be easily carried out by a normal processor while the latter required a dedicated coprocessor.

The algorithm required a 56+8 bit key (8 parity bits do not increase security) and operated on 64 bits data blocks. This means that to encrypt a message longer that 64 bits, it has to be split in multiple block (more on that later).

Triple DES (3DES)

Since the normal DES was found to be easily attacked, a new version was introduced. This new version increased the security using the basic DES algorithm multiple times.

3DES has the advantage that remains compatible with normal DES if alle the keys used are equal to each other.

There are two variants of 3DES:

2 keys 3DES

This algorithm uses two keys and which are used as follows:

1. The plain text is encrypted with the first key to obtain a first cyphertext: .
2. The cyphertext created in the previous step in encrypted again with the second key:
3. The final cyphertext (the one that will be sent to the receiver) is obtained encrypting the cyphertext from step 2 with the first key:

3 keys 3DES

This algorithm uses three keys , and which are used as follows:

1. The plain text is encrypted with the first key to obtain a first cyphertext: .
2. The cyphertext created in the previous step in encrypted again with the second key:
3. The final cyphertext (the one that will be sent to the receiver) is obtained encrypting the cyphertext from step 2 with the third key:

Meet in the middle attack

Double DES does not exists because it would be subject to a meet in the middle attack. If in DES we use a key of length , in 2DES we would have a key of length but the meet in the middle attack would reduce the effective key length to (basically you double the amount of work to encrypt the message and you get the same result as adding only 1 bit).

How it works

• Hypothesis:
  • The keys and are bits long
  • There is a know plain text/cypher pair such as . This can be easily obtained if the attacker is able to use the encryption algorithm with a chosen plain text.
• Actions:
  • Compute all the possible values and store them with the key that generated them.
  • Compute all the possible values and store them with the key that generated them.
  • Search among all the stored values the ones with and retrieve the keys that generated them.

Block algorithms

As anticipated before, many algorithms can only be applied to fixed size blocks: this implies that longer data has to be split before the algorithm can be applied.

Here we will discuss two modes of operation.

Electronic Code Book (ECB)

In ECB the blocks are encrypted individually: and then sent one after the other. The decryption is extremely simple and consists in using the decryption algorithm on each block: .

This mode has the advantage of being fast and parallelizable (the blocks can be encrypted individually without needing to know anything else).

Even considering said advantages, this mode is very weak, specifically on long messages, because the attacker can precompute of a known with all possible keys and then compare the results with the blocks sent by the victim. Even though such an attack seems difficult to perform (it requires to know what message the victim will send), it is instead quite easy: consider that most file types have a constant heading that gives information about the file itself, and thus the attacker can easily guess the content of one of the blocks.

Another problem of ECB is that the receiver has not way of knowing if the blocks were mixed or if some of them were deleted.

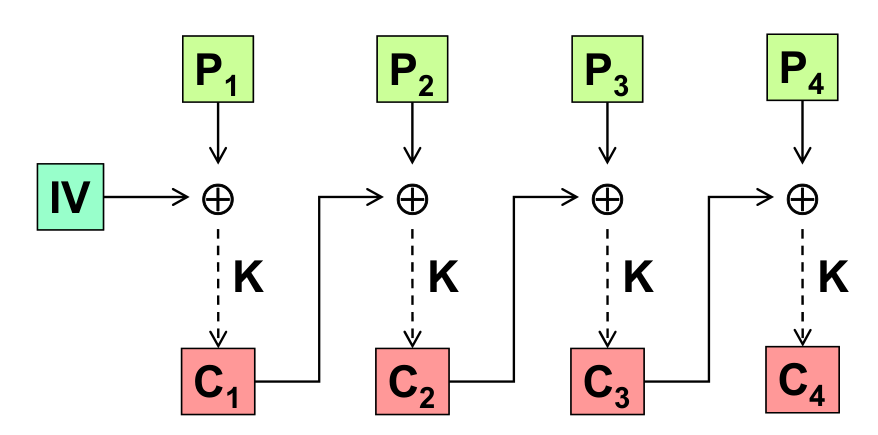
Cypher Block Chaining (CBC)

In this mode the blocks are not encrypted individually but each of them contributes to the final cypher, making the previous attack unfeasible. The i-th block is obtained as follows: .

Since the first block would be subject to the same attack seen before, it is important to add an initialization vector (IV) chosen at random which has to be sent as well to allow the decryption.

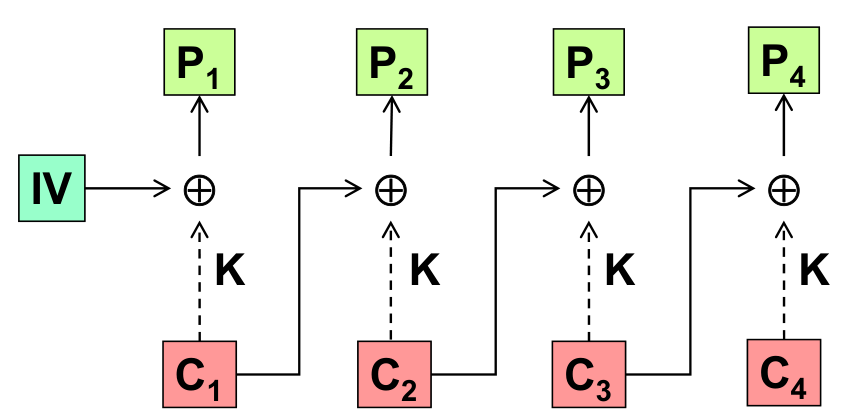
The decryption phase in this case is not trivial: . The receiver needs to know = IV.

Padding

Complementarily to what said before, if the data to be sent is shorter than the block of the algorithm, it has to be “enlarged” to be able encrypt it. The problem that arise are that more data than necessary has to be sent and that the padding bits need to have a standardized value.

The padding bits can be chosen in many different ways, for example:

• All 0s (this method requires to know the length of the message in advance to be able to distinguish the “good” bits from the padding).
• One 1 bit followed by many 0s (used in DES).
• One byte with value 128 followed by 0s.
• Last byte with value equal to the length of the padding. This method requires to define what is the value of the other bits, again multiple options are available:
  • All 0s.
  • All bytes with the length of the padding.
  • Random bytes (can increase security since the attacker has no way to extract any information about the size of the padding).
  • Each bytes contains a progressive number from 1 to the length of the padding.
  • All bytes represent the length of the padding - 1.

Some types of padding can offer minimal integrity control (for example if the data is manipulated or the key is wrong the the length of the padding would be incoherent). Padding is usually used on the last block of large data and, in case the data length is an exact multiple of the block, it has to be added for consistency.

Cyphertext Stealing (CTS)

todo

Counter Mode (CTR)

todo

Symmetric stream encryption algorithms

This kind of algorithms works on a data stream without requiring the split in block, instead it operates on one bit or one byte at a time.

The ideal algorithm of this kind is the one-time pad: this algorithm requires a key which is:

1. As long as the message to be sent
2. Single use
3. Pre-shared between sender and receiver

The encryption function is a simple XOR between the plain text and the key. As it’s easy to imagine, this algorithm is not practical at all but it provides maximum security.

In real algorithms a pseudo-random key generator is used to generated keys that are synchronized between sender and receiver. Modern algorithms of this kind are Salsa20 and ChaCha20.

Symmetric encryption problems

Symmetric encryption has two important flaws that have to be acknowledged.

The first one is that if a message has to be shared between two parties, they need to share a common private key just for their couple; if someone has to send a message to a restricted group, the key has to be shared among all the members of that group.

The second problem concerns the key distribution: since each couple needs its own secret key, parties would need keys to be able to communicate with each other. Furthermore the keys cannot be exchanged on the same (unsecure) channel where the communication happens, otherwise everybody would be able to see them. This means that the key exchange has to happen Out-Of-Band (OOB), for example in person. This is obviously not feasible and thus a solution has to be found.

Asymmetric/Public-key cryptography

In public-key cryptography (PKC), instead of having a single key shared between sender and receiver, a key pair is used. The two keys are not independent: if one of them is used for encryption, the other one must be used for decryption.

Compared to symmetric cryptography, asymmetric cryptography has a much higher computational load and for this reason it’s commonly used for encrypting the keys of a symmetric algorithm before sharing them.

The keys are generated in pairs: one of them, the secret key () is kept by the owner, the other one, the public key () is shared with everybody. The reasons for this will be clear in the following.

Do to how the algorithms are created, a message encrypted with can be decrypted only by the corresponding and vice versa. This allows us to use the same algorithm for two distinct goals.

Confidentiality without shared secrets

PKC allows anybody to generate a secret message for a particular receiver provided that they know its public key. To do that the sender has to encrypt the plain text with the receiver’s public key; this message can be decrypted only by the receiver since it is the only one with the right private key.

Digital signature

Digital signature provides a way for someone to authenticate a message and provide integrity. Digital signature work in the opposite way compared to what we saw previously. In this case the sender “signs” the message by encrypting it with its private key, the receiver then uses the corresponding public key to verify that the message was really sent by the real sender (who is the only one with the correct private key).