Fermi surfaces and e transport

Fermi surfaces

The Fermi surface is the surface of constant energy in space. It separates the filled orbitals with the unfilled ones at .

todo

Current transport in solids

todo add drawing

The current density is given by

If is the electron density, then where is the velocity of the electrons.

From the relation above we can write and substitute this in the formula for the current density, getting:

or, in vector format

Electrical conductivity for free electrons

Kittel, Chapter 6, "ELECTRICAL CONDUCTIVITY AND OHM’S LAW"

In the case of a free electron

If we ignore the effect of the magnetic field () we can derive

which, integrating over we get

If at (before any force is applied), the electrons occupy the states inside the Fermi sphere cantered at , when the force is applied the sphere will move as a whole (the force increases the momentum of all the electrons in the same way).

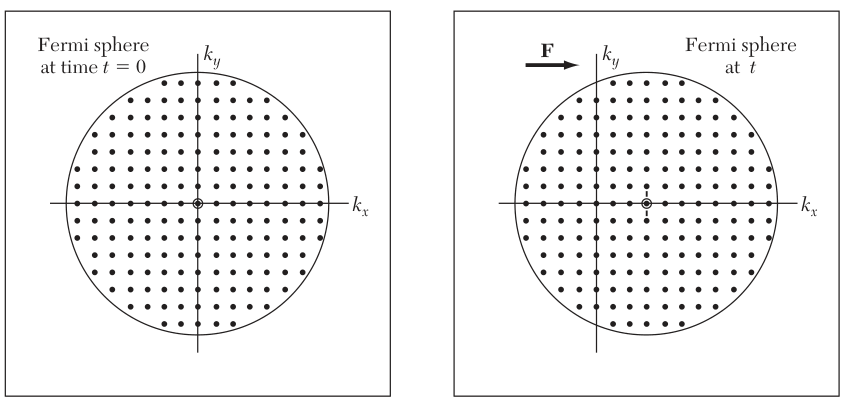
Since the electrons will collide with impurities, lattice imperfections and phonons, their momentum will not grow indefinitely.

If we call the mean collision time, we can write

which represents how much the sphere is translated when the force is applied (picture above on the right).

The incremental velocity of the electrons can thus be written as

So, going back to the current density , if we are in a constant electric field , we have

which is Ohm’s law.

The electrical conductivity

can be understood intuitively considering the following things:

• We expect the charge transported to be proportional to the charge density .
• The factor is given by the fact that the acceleration in a given electric field is proportional to and inversely proportional to .
• The time describes the free time during which the field acts on the carrier.

Semiclassical description

For a more accurate description we would need to solve the the time dependent SE (which is complex to do). So we describe the electrons as wavepackets: linear combination of plane waves with a wave vector in the interval

where is the dispersion relation.

The mean motion of the wavepacket is given by the group velocity

Since we are in a crystal, the wavepacket is formed by the combination of Bloch states (called Wannier functions). The electrons velocity will be given by the group velocity of the Bloch wavepackets (todo why is this true?):

In this case is a sort of mean wave vector that characterises the wavepacket.

If we now want (todo why should we want to) to calculate the acceleration along the i-th direction we get

We can rewrite

By substituting this in we get

Finally, we get

Effective mass tensor

When the effective mass doesn’t change depending on the direction, it can be written as

which shows that the effective mass is related to the curvature of the dispersion relation.

todo improve plot

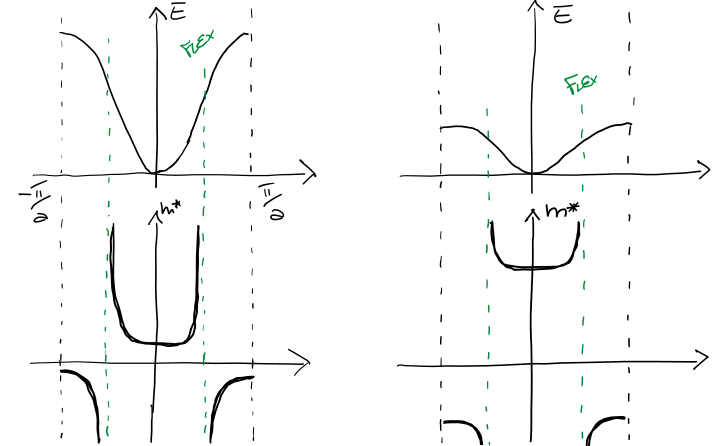
Current inside an energy band

Full band

The electron density associated with a volume centred around is

and the current density is

To evaluate the total current density we need to integrate on the 1st BZ:

Since is a periodic and even function, will be a periodic and odd function. This means that its integral over the BZ is null.

todo page 22 bianco: why calculating the velocity

Partially filled band

In case the band is not full, the electric field can change the electron’s momentum, which means that the distribution of s around is not symmetric anymore.

In this case

Similarly to before, can be calculated by integrating, in this case only over the occupied states ()

This means that the current density in a partially filled band can be seen as if it was due to positive charges (holes) in the band.