Group A waveguides

Optical waveguides are devices that restrict the directions of propagation of light to 1 or 2 dimensions. We will mostly deal with planar waveguides (or slab waveguides) which, as the name suggests, allow the transmission of light in 2 directions only.

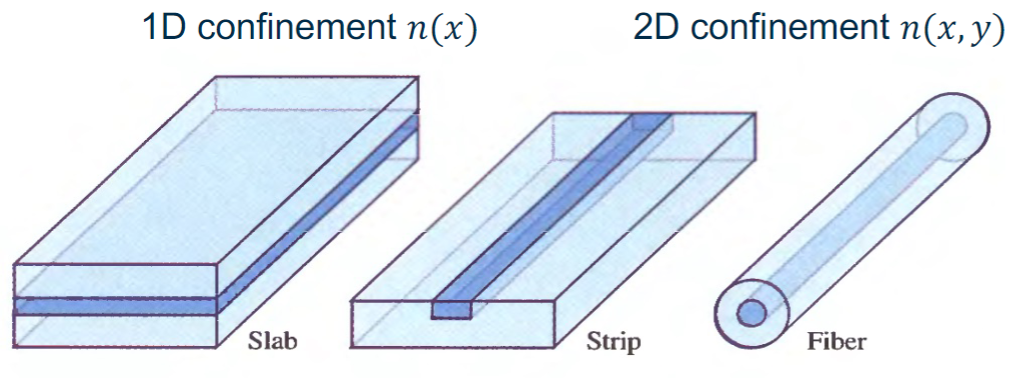
Slab waveguides

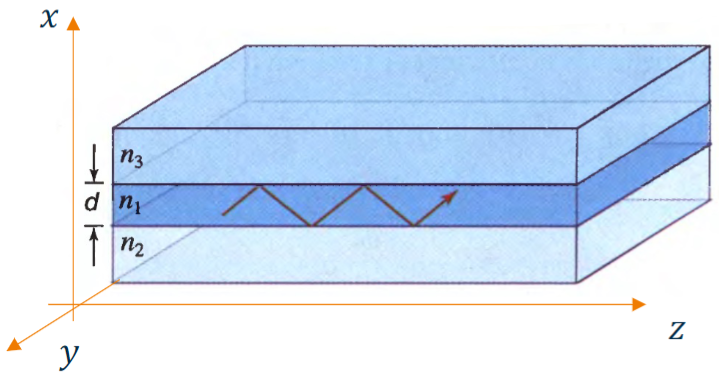
Slab waveguides are composed of three layers of materials which need to have the right optical properties to guarantee total internal reflection. In the image below we can see that we have one layer of core (refractive index ), which is the material where the light will travel through, and two layers of cladding (refractive indices ). In order to have total internal reflection we need the following conditions to be satisfied:

The two layers of cladding do not need to have the same the refractive index and can also be completely different materials (even air in the second case in the image above).

We will assume that the slab waveguide has infinite extension in the two directions and .

Transverse modes

In the following we will limit our study to transverse modes, which is to say solutions where the amplitude does not depend on the propagation direction of the wave (in blue below).

We will also study monochromatic waves (we will have one single frequency ).

The subscript is called mode number and distinguishes the different possible solutions, the mode propagation constant is unknown since we are not dealing with plane waves.

Will will only study the cases where the materials are linear, isotropic, homogeneous, transparent and non-magnetic. To simplify our study will will also consider (i.e. same cladding on both sides).

Transverse electric modes

In the transverse electric (TE) modes, we will assume that the electric field is orthogonal to the propagation direction: . The same considerations can be done in the transverse magnetic (TM) modes but we will not go into the details of this case.

Some of the parts marked as optional in the slides are omitted

Eigenvalue equation

Studying the Maxwell equations after imposing the constraint that leads to a single equation for the non zero component of the electric field called eigenvalue equation:

can be used to determine ( i.e. the eigenvectors) and (the eigenvalues).

and is the layer dependent refractive index.

This eigenvalue equation can be satisfied by two families of waves: guided modes (where light is confined in the core) and unguided modes (where light is not confined).

We are only interested in the study of guided modes because we want to use the waveguide as a way to force the light along a specified path. Since we are studying a real case, we have to remember that we are not in the ideal case of total internal reflection but we will have some amount of “leakage” of the waves in the cladding, for this reason we talk about evanescent waves, which is to say that their intensity vanishes for .

Boundary conditions

Before proceeding we need to remember that we have to impose boundary conditions at the interfaces between the materials, which is to say impose the continuity of the fields in and .

Guided modes

By solving equation we find that in order to have guided modes we need to satisfy the condition

furthermore we find that we have discrete solutions for different values of as we can see from the plot below.

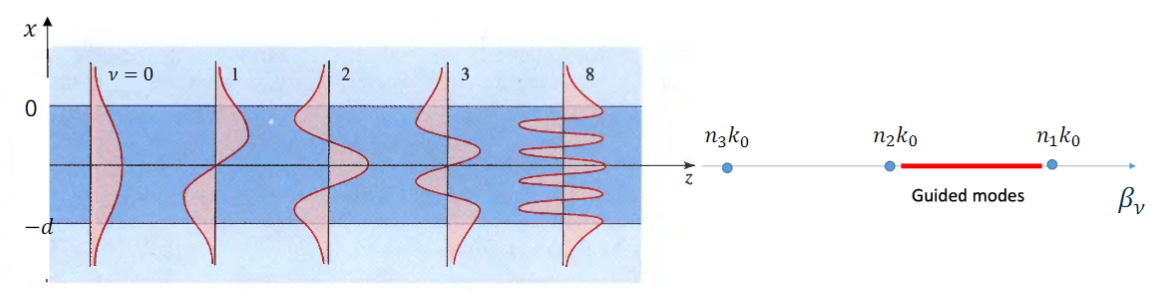
We can also notice that, independently of the mode number the waves always vanish for as expected. If, on the other hand, varies outside the range stated above, we get radiated or unguided modes, where the waves are not confined in the core.

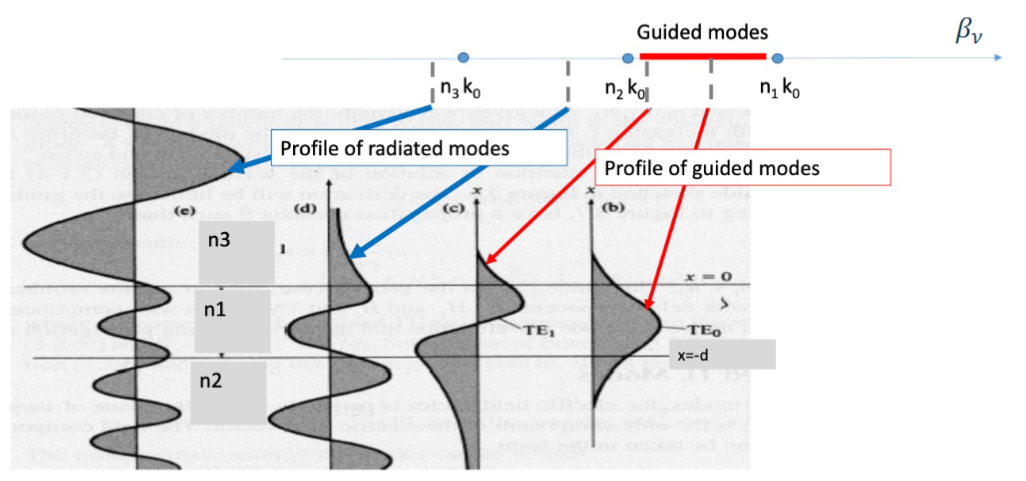
Among all the possible modes we can recognize the fundamental mode () which has a Gaussian shape and is always present (while modes with might present or not depending on the properties of the waveguide such as thickness, refractive indices, frequency, etc.)

Consequences

One important consequence of this result is that, since the TE modes form a complete and orthogonal functional set, i.e. a basis, any TE electric field can be represented as a linear superposition of TE modes.

todo explain the slide

Examples

todo explain the slide

Two dimensional waveguides

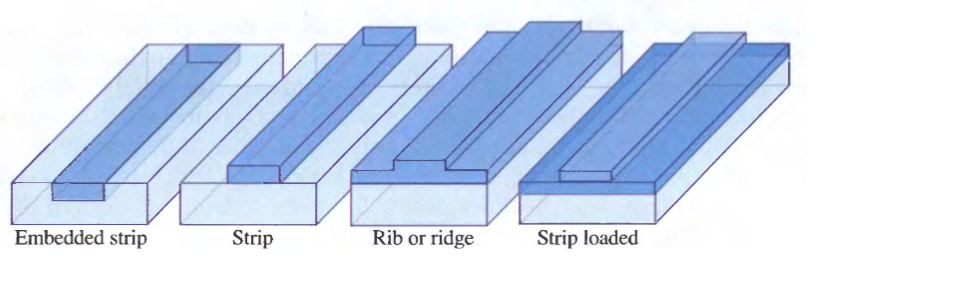
In 2D waveguides light is confined in two dimensions (see image at the top of the page). In this case we cannot solve the Maxwell equations analytically as we did for the slab waveguides but we have to use numerical methods such as the Finite Elements method or the Effective Refractive Index method.

The image below shows an example of such analysis. We can clearly see that the waveguide successfully accomplishes the goal of confining light in a limited region but we can also see that this confinement is not sharp.

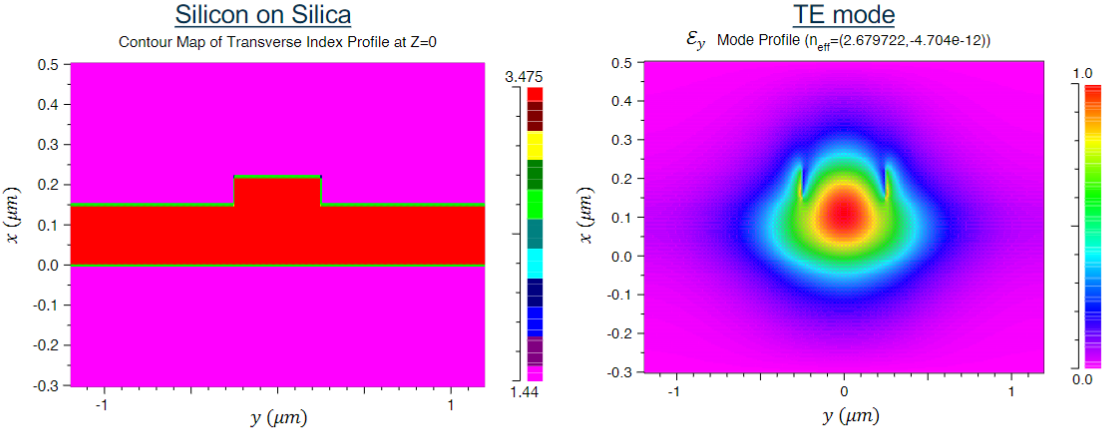
Parameters

In the following we will study some of the properties that characterize 2D waveguides.

Chromatic dispersion

Chromatic dispersion is strictly related to the fact that the group velocity dispersion (defined below) depends of the wavelength of the light travelling in the medium. This effect results in the broadening of the initial input.

The group velocity is defined as follows:

And can be intuitively seen as the velocity of the “peak” of the wave (for example when thinking about a gaussian).

Since the group velocity depends on frequency. This is known as Group Velocity Dispersion (GVD).

todo what is ?

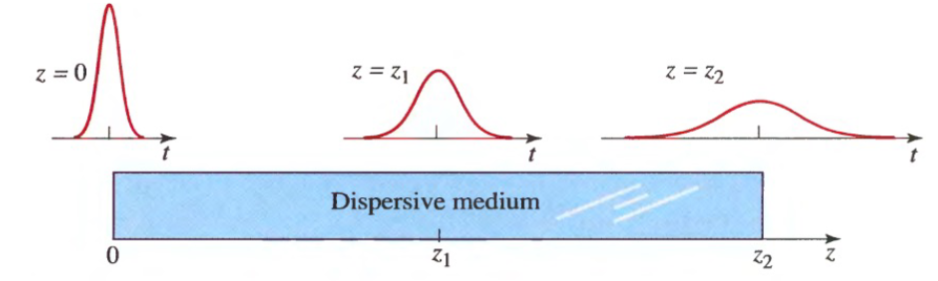
todo write the last parts