Phonons

In this section we would like to describe the properties of the atoms that make up the crystal.

In the Born Oppenheimer approximationtodo we described them as fixed in place but now we want to make a more precise analysis.

We start by modelling the atoms with a mass-spring system like in the image below

todo

In 1D we have the Hooke law:

with the spring constant. The potential is given by

Nomenclature

We identify the position of a primitive cell with a translation vector and the real positions of the atoms inside the primitive cell with another translation vector (which has the origin at the origin of the primitive cell) with :

• The -th primitive cell is identified by
• Atoms are identified by Greek letters
• The crystallographic directions are identified by

This means that the position of the atom in the cell is

We also need to introduce the term which represents the displacement with respect to the equilibrium position, so that we can write

We call the potential energy with respect to the equilibrium position.

If we work with the component we can expand in Taylor series the total energy of the crystal . We neglect the higher order terms, getting what is known as harmonic approximation.

where

are called coupling constant,

They have the dimensions of spring constants and serve to generalize the spring constants of the harmonic oscillator to a system with many degrees of freedom. (Luth, 4.2)

We can write the force acting on atom in the cell along the direction, caused by the displacement of the atom in the cell along the direction as

Equation of motion

If we call the mass of the ion we get the following equation of motion

which is the generalized version of

If we have primitive cells and atoms in the basis we would have differential equations that describe the movement of the atoms.

We are going to impose (todo why?) the solution

where is the wave vector and is the normalization constant and is proportional to .

What we want to do now is to calculate the second derivative of and substitute it inside the equation of motion, getting (calculations omitted):

where

is the interaction matrix and is independent from

Equations (which are a system of equations) describe what happens to the single atom along the direction with respect to the movement of all the atoms along the directions . To solve the system we need to have that

We call dispersion curves or dispersion branches.

If (only one atom inside the base) we have equations and thus dispersion branches, called acoustic branches. If, on the other hand, (more than one atom in the base) we will have dispersion branches, out of which there will be acoustic branches and optical branches.

Normal modes for 1D monoatomic chain

In this case we have a monoatomic linear chain of atoms which are allowed to move in the horizontal direction only. Each atom has mass and represents the displacement of the atom .

The atoms are modelled as a mass-spring system with springs with elastic force constant .

Equation of motion

The equation of motion for the atom is given by

Where the three terms represent the contributions of the atoms , and respectively. To proceed with the calculation we need to calculate the individual terms:

Substituting the three orange expression that we got graphically we get:

The solutions are in the form: #todo why?

If we apply the BVK conditions (i.e. the atom is equal to the atom and ) we get:

which is satisfied when with . This leads to

where is the length of the chain.

If we substitute these results into the equation of motion we get (calculations of the derivatives omitted):

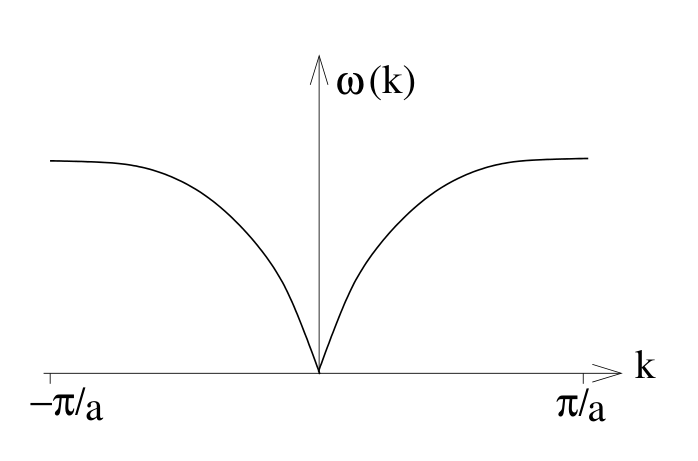
Along the chain we have propagating waves with:

• Phase velocity:
• Group velocity:

For we can approximate the linearly getting

which is the typical behaviour of acoustic waves.

Normal modes for 1D bi-atomic chain

This case is similar to the one before but the lattice, in this case, is composed of 2 different atoms.

The process is the same as before but now we need to take into consideration that we are dealing with 2 different kinds of atoms and thus we will have two equations of motion:

which can be solved similarly to before (BVK, etc) getting a system of equation that can be solved by imposing the determinant of its matrix equal to 0:

The solution we get is

which, similarly to before, has a periodicity of

---

Where we introduced the constant

For the optical branch, in , the displacement of the atoms in every unit cell are identical. The sublattices of light and heavy atoms are vibrating against one another (as visible in the two images below).

todo finish last part