Quantum computing

Quantum gates

See also the corresponding notes for the Qubit Electronics course

NOT

The NOT gate is represented by the matrix

and acts on a state as follows:

it is easy to see that the effect of the gate is the expected one, which is to say flip the initial state.

Constraints for quantum gates

From the example above we saw that a gate acting on a single qubit can be represented by a two by two matrix. Due to the fact that the state after the application of the gate must remain normalized, the matrix must be chosen in such a way that if then . Where is the state after the gate.

It turns out that for this condition to be satisfied the matrix that describes the transformation must be unitary, i.e. . This is the only constraint on quantum gates.

Z gate

The gate is described by the following matrix

The effect of this gate is to leave unchanged and flip the sign of to give .

Hadamard gate

The Hadamard is described by

and can be thought as being the “square root of the NOT gate” in the sense that it turns into , which is half way between and (first column of ). The same thing is done for , which is turned into .

It is important to notice that , in fact .

Looking at the effect of the Hadamard on the Bloch sphere this corresponds to a rotation about the axis by , followed by a rotation about the axis by .

Link to original

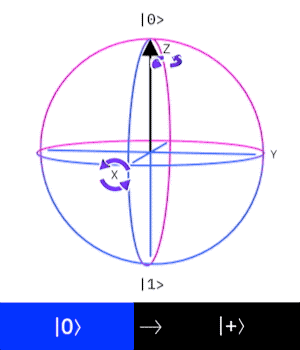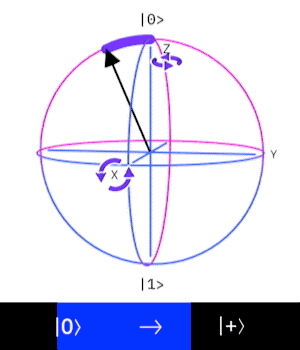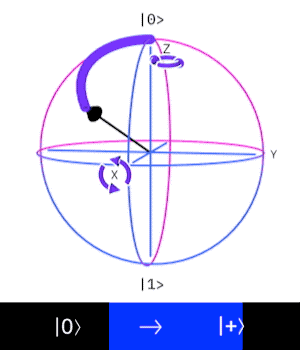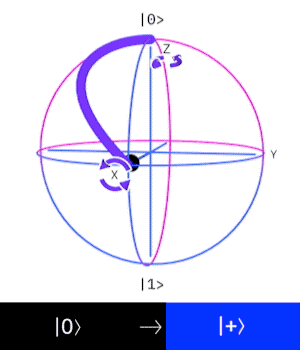
Controlled NOT (XOR)

This gate has two input qubits, known as the control qubit and the target qubit, respectively. The circuit representation for the CNOT is shown in the image below; the top line represents the control qubit, while the bottom line represents the target qubit. The action of the gate may be described as follows. If the control qubit is set to 0, then the target qubit is left alone. If the control qubit is set to 1, then the target qubit is flipped.

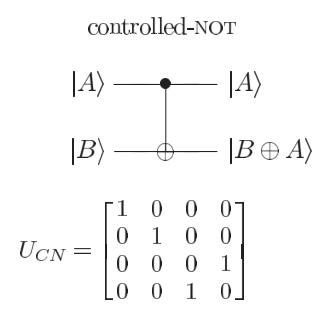
The CNOT gate is particularly important because any multiple qubit logic gate may be composed from and single qubit gates.

Controlled operator C-U

Similarly to what happened for the CNOT, we can extend the concept of “control” to any other unitary operator . In Dirac notation, the controlled version of the operator can be written as:

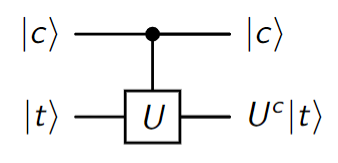
In computational basis, the matrix representation of the C-U operator is given by

with

No-cloning theorem

The no-cloning theorem state that it is not possible to create a copy of an unknown quantum state. This statement can be proved using the following reasoning.

Suppose we have a copying machine with two slots. The machine starts with a pure quantum state in the data slot that we want to copy to the target slot which, initially, is in the pure state . At the beginning of the experiment the machine is in the state

If the copying procedure can be described by some unitary evolution , we can write the following:

If we apply the copying procedure to two particular pure states and we would have

If we take the inner product of these two equation we get

Since is satisfied only for and we must have either or . This shows that the device can only clone states that are orthogonal to each other.

Even though this proof holds only for unitary operators, it can be shown that the results remain valid for the general case as well.

Teleportation

Superdense coding