Introduction to quantum optics

Brief introduction to communication

Shannon-Weaver model

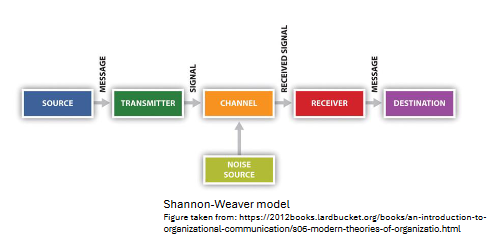
The basic concept of communication can be represented by the Shannon-Weaver model. The idea is that communication is a linear one-way process, involving six elements: The source of information, the transmitter that sends a signal to the channel (affected by noise); the signal reaches the receiver which delivers the information to the destination.

Analog vs Digital signals

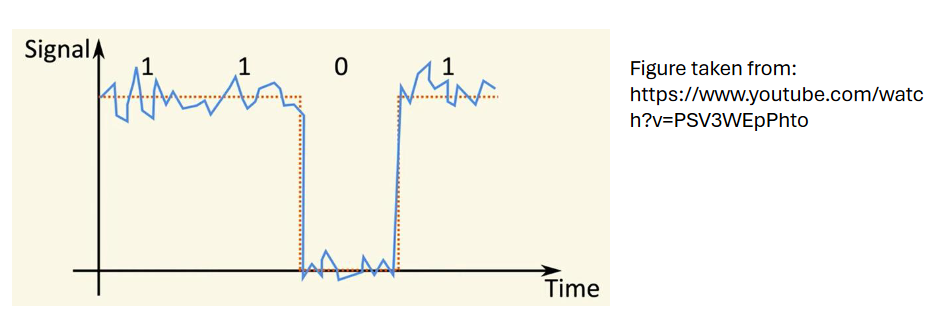
Analog signals are continuous signals varying with time: the signal (S) is generated by encoding the message (T a time-varying quantity) in some time-varying signal and sent to the receiver. The signal (S) is decoded in order to obtain some information about the original message (T) The two main problems with analog signals are the susceptibility to noise and the difficulty to copy them.

Instead digital signals are generated by encoding a discrete set of values, the accuracy depends on the sampling rate and they show more advantages compared to the analog ones: are less affected by noise, cheaper to produce, easier to process and the bandwidth is easier to manage.

The classical unit for a digital signal is called “bit” and follows the usual representation of 0/1. This notation generally is the representation of an electrical signal with two possible values; even introducing some noise the bit is more robust compared to an analog signal.

Quantum communication

Quantum mechanics offers both superposition and entanglement to exploit in new communication systems. To have a better understanding on notations and representations of qubits that will be used in the following notes, is recommended to look at:

• Bloch sphere: Condensed Matter lecture about qubits
• Dirac notation: Formulas from QMPI
• Gates: Q Electronics introductive lecture

Measurements

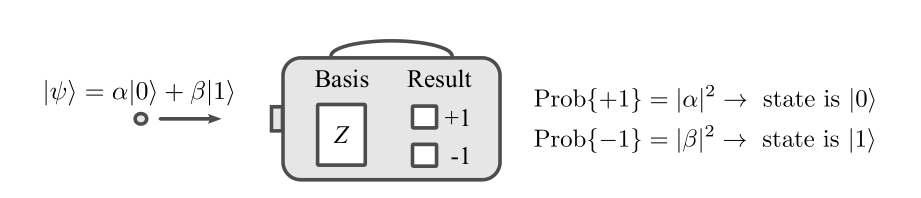
A measurement extracts information from a qubit, basically tells us if the qubit is in the state or in the state .

Measurement in the Pauli Z basis

Considering the measurement as a big box, fed with the prepared state, a general one could be . There are two possible values as measurement outputs, and we will assign them the values of and . The probability of these outcomes, corresponding to state and state are given by their probability amplitudes. Immediately after the measurement the state collapses either onto or onto :

Quantum Communications, M. Hajdusek and R.Van Meter

This particular measurement is referred as measurement in the computational basis or in the Pauli Z basis.

Measurement in the Pauli X basis

The measurement can be done in other basis, like the X basis, looking at the probability of finding the qubit either in state or .

With (obtained from simple algebraic passages) the measurement probabilities are the ones in the picture

Like before, the measurement collapses the qubit’s state either in or

Basis and inner product

From linear algebra: a basis is a set of vectors that allows you to write down any other vector.

The generic state can be written in terms of the states and (Pauli Y basis), as well as in the X basis as we saw before. The state is not changed but just the representation of it.

An important concept is the inner product, is basically a dot product between two vectors and tells us the “overlapping” between two quantum states. A bra is needed for the product, and is defined as the adjoint of a given state

The inner product between and is:

The state is normalized when Two states are orthogonal when

The inner product can be used to calculate the probabilities of different outcomes when measuring the state in a particular basis.

Probabilities

The measurement of a qubit is a single shot measurement; in order to obtain some information about the probabilities, many measurements should be performed on copies of the same state. In the case of the box mentioned above of the measurement in the Z basis the number of outcomes "" will be denoted by and the number of outcomes "" will be denoted by . Intuitively the ratio between the number of one outcome and the total number of measurements will be approximately equal to the probability of obtaining said outcome:

Expectation value

In the Pauli Z basis:

in Dirac’s notation:

Variance

The outputs of the measurements are random, some degree of variance is expected:

Thus in the Pauli Z operator is:

Multiple Qubits

Two classical bits can be in four different states: .

Using Dirac’s notation: there are still four possible states.

Any general state of two qubits can be written as a superposition of those four possible states, weighted by their respective probability amplitudes :

The state must be normalized:

In vector notation these kets are:

We can easily see that are orthogonal to each other, and that they form a basis for the space of the two-qubits states, the general superposition in vector notation is:

Tensor Product

The tensor product is the mathematical concept that allows us to construct the vector representation of the two qubits given the states of the individual ones. The symbol that denotes the tensor product is .

or equivalently:

Noise

A new formalism is needed to consider the effects of noise in quantum communications or noise in the state preparation.

Outer product

The outer product is defined as: