Quantum Wire

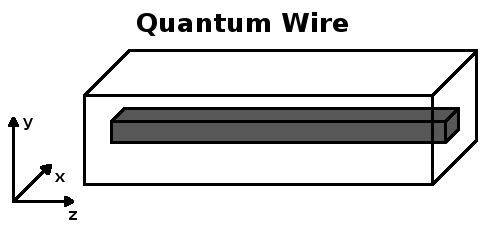
There is a general rule that applies to confined structures: if the number of degrees of freedom is denoted by and the number of directions of confinement is denoted by , then

In a quantum wire we have

Which is to say that we have 2 dimension of confinement and one degree of freedom for the electrons.

Let’s start from the Schrödinger equation

We separate in components the potential:

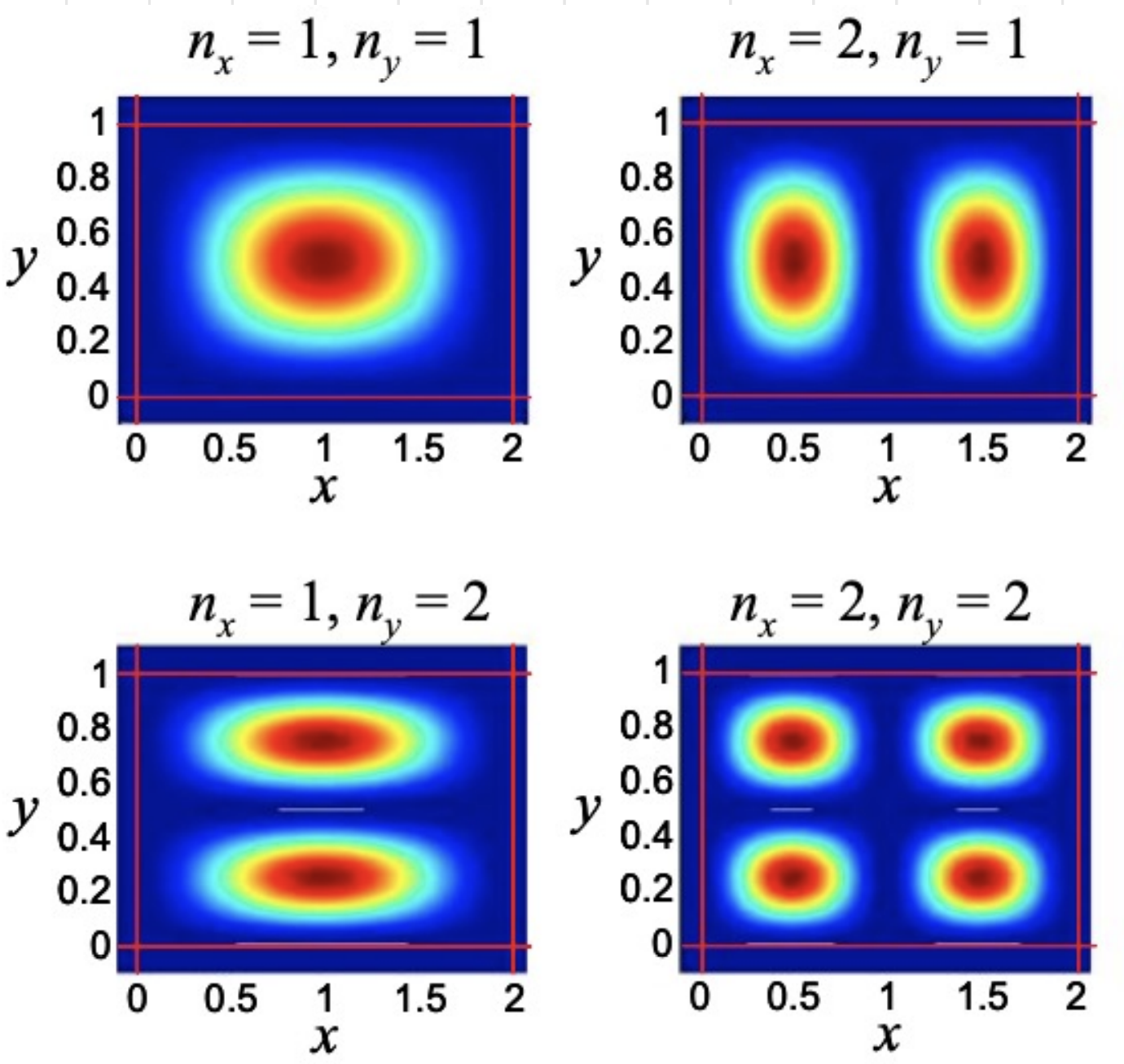
As we did before (in other scenarios) we solve separately the three dimensions and we sum up the energies and multiply the wavefunctions to get the overall solutions. What we will find is that we have a free particle in the direction and an infinite potential well in the and directions.

Along direction:

Along directions, due to the fact that the potential goes to the infinity at the edges we have the boundary conditions:

so the solutions are:

These (unlike in ) are stationaries waves. They do not propagate in space but they are confined in

The total energy will be:

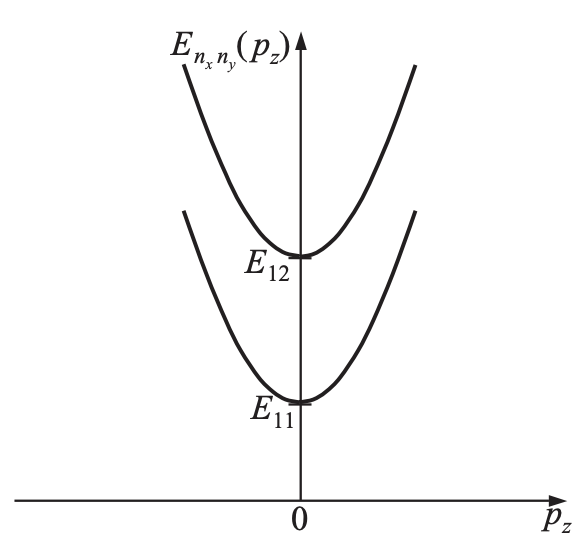
How many states are there in the parabola? To calculate them we need to apply conditions also in the direction. The typical conditions that we apply when we want to avoid to deal with surfaces are periodic boundary conditions.

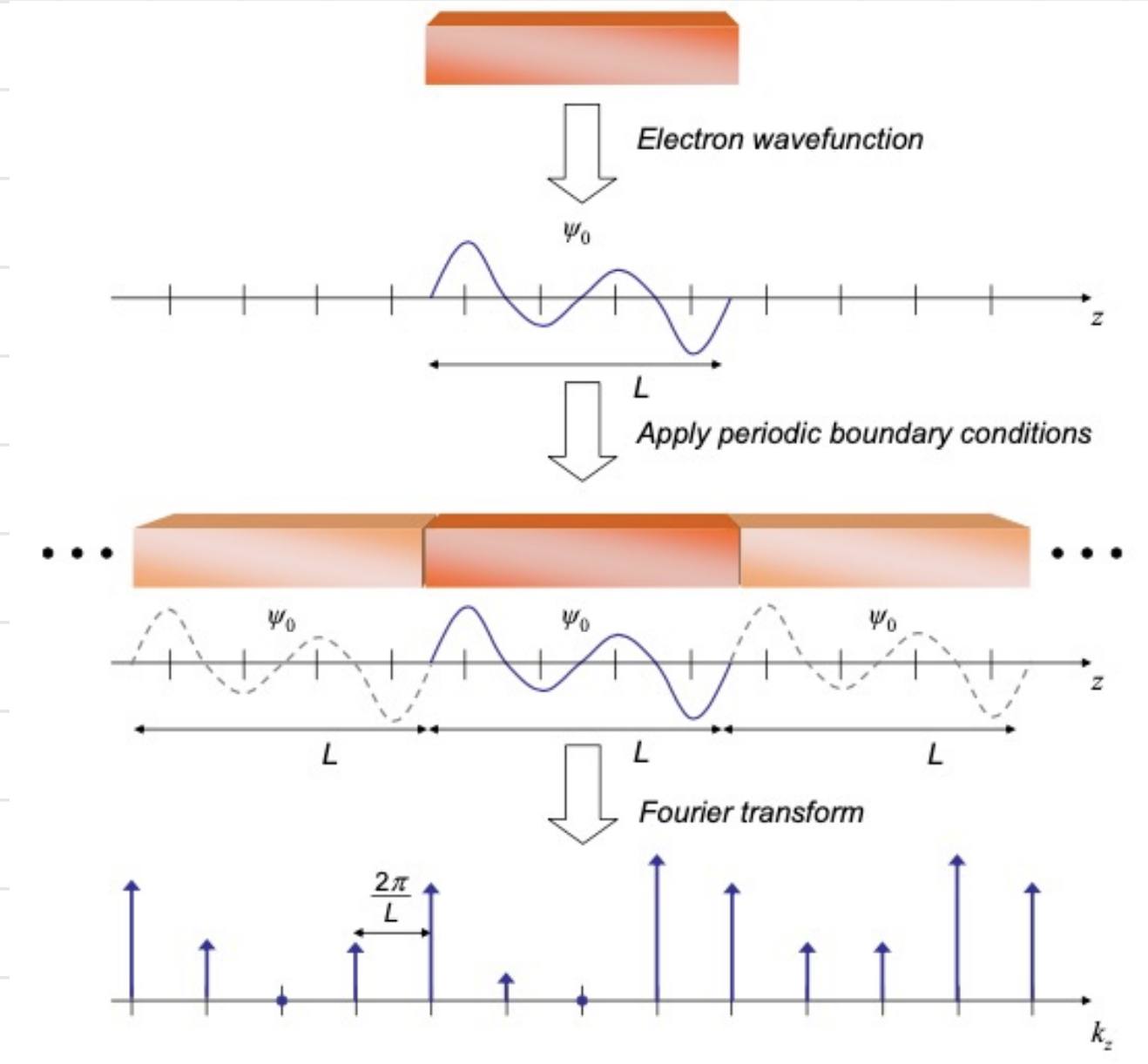
Due to the boundary condition we get that:

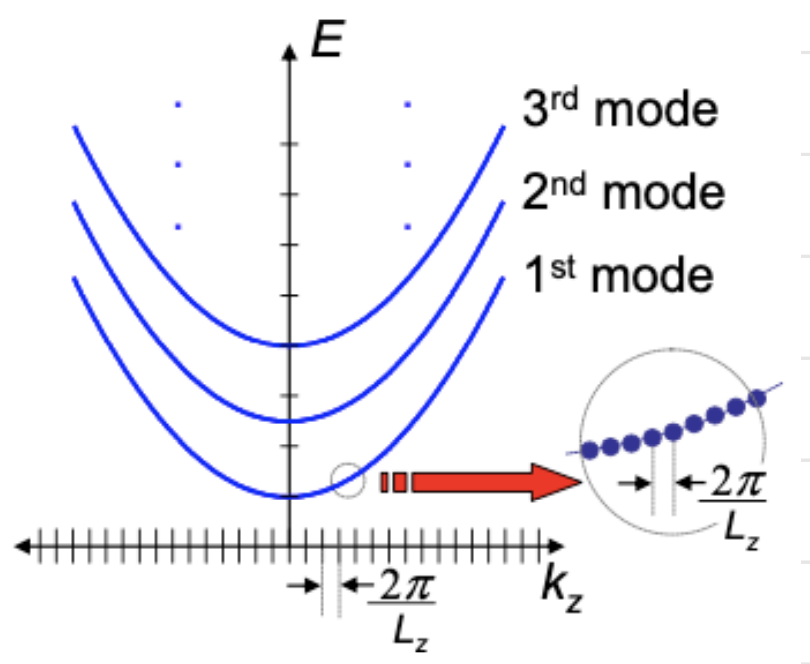
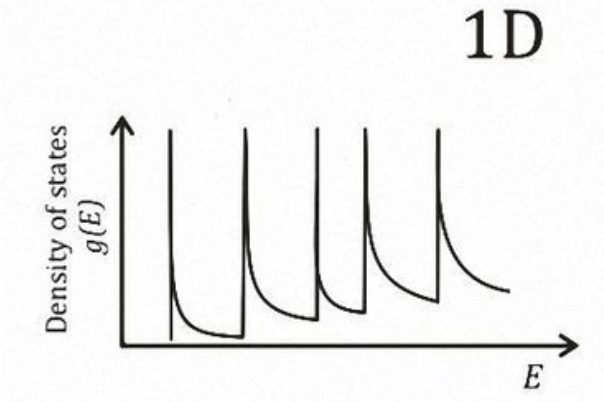
1D DOS

Starting from the first band we can write:

We can find geometrically reasoning on the following picture.

Recalling the relation between and we get:

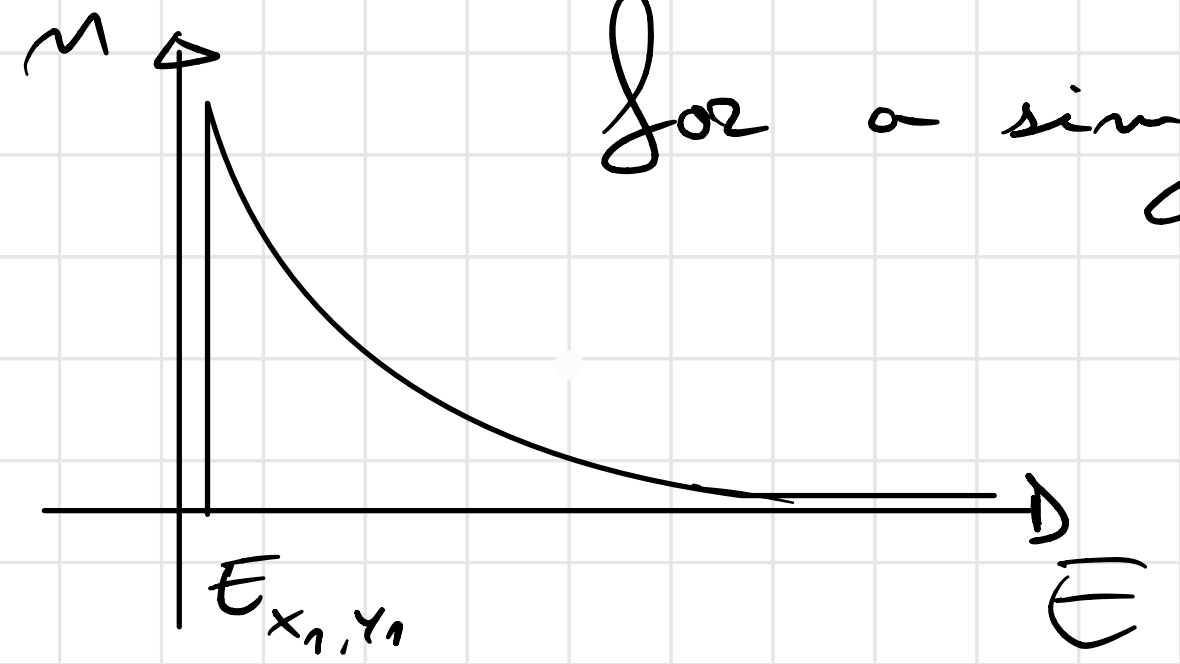
We can now add the other bands