Aharonov-Bohm effect

The Aharonov–Bohm effect is a quantum-mechanical phenomenon in which an electrically charged particle is affected by an electromagnetic potential despite being confined to a region in which both the magnetic field and the and electric field are zero. The most commonly described case, sometimes called the Aharonov–Bohm solenoid effect, takes place when the wave function of a charged particle passing around a long solenoid experiences a phase shift as a result of the enclosed magnetic field, despite the magnetic field being negligible in the region through which the particle passes.

The AB effect shows also that is not strictly related to , and that is not only a mathematical trick to solve Schrödinger equation in a simpler way but a physical quantity.

Aharonov–Bohm solenoid effect

A solenoid generates a magnetic field only in the inner part of the loop, thus in the ring arms (in grey) there is no . Since is not unique with respect to , we need to select a suitable for our problem and we use the Coulomb gauge:

We notice that any close line of that includes the inner solenoid spans an area that includes the entire magnetic flux .

Thus since we know that we can write that :

and for Stokes theorem we have also that:

From these relationships, we can get the information that there are regions in space where the value of is zero while the value of is not. To show this, we can examine the following two cases:

First case ()

Second case ():

we can plot versus and it becomes evident that there are regions in space where the value of is zero while the value of is not:

Schrödinger equation of the system

We start from the general Schrödinger equation like in the case of the Quantum Hall effect :

But this time instead of replacing with the form given by gauge we use a gauge transformation that is a modification of the wave functions and potentials in a way that leaves the physical predictions of the theory unchanged

This changes the Schrödinger equation but not the physical predictions (expected values).

Let’s see how such a transformation can simplify the mathematical form of the Schrödinger equation

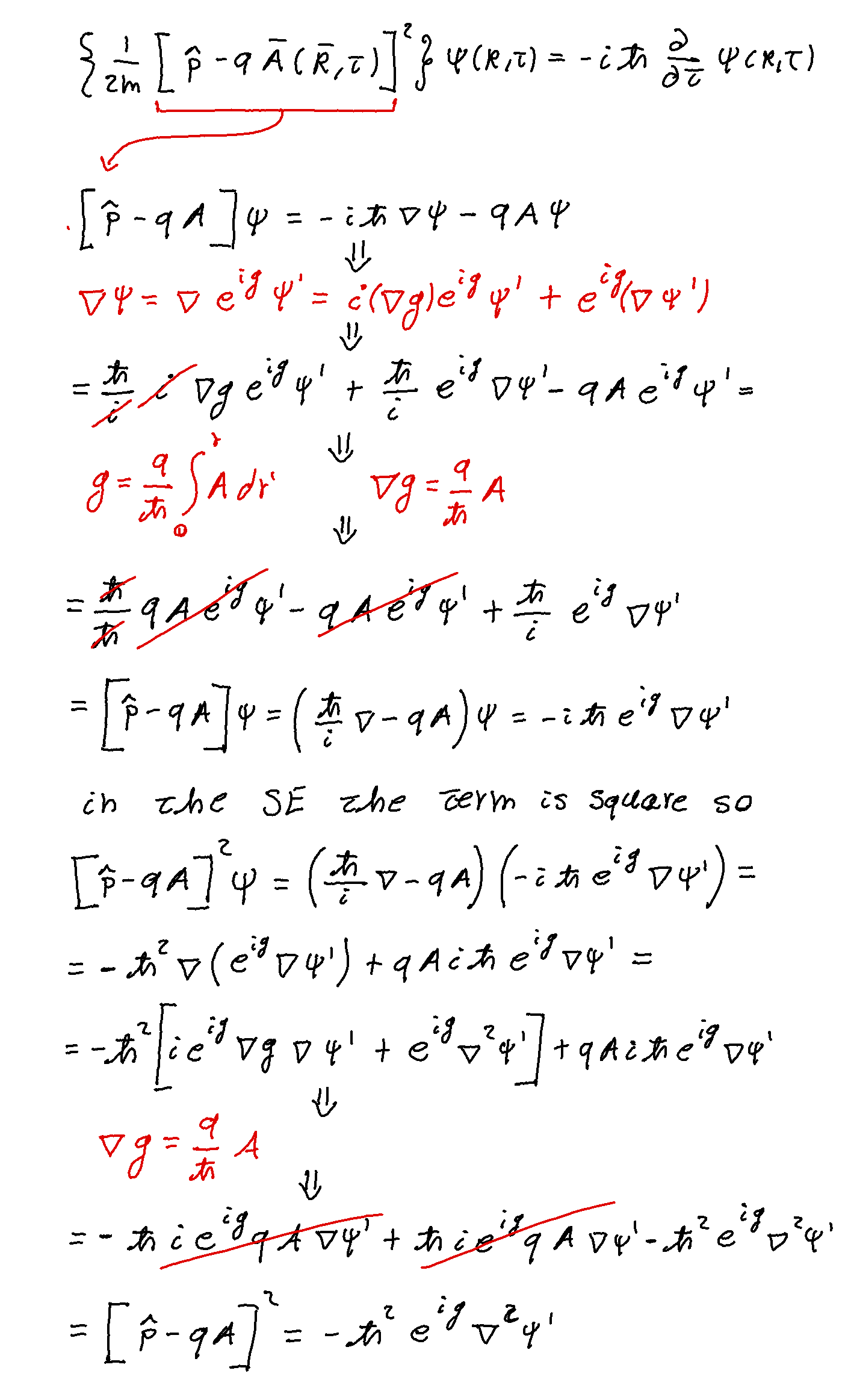
Substituting in the Schrödinger equation:

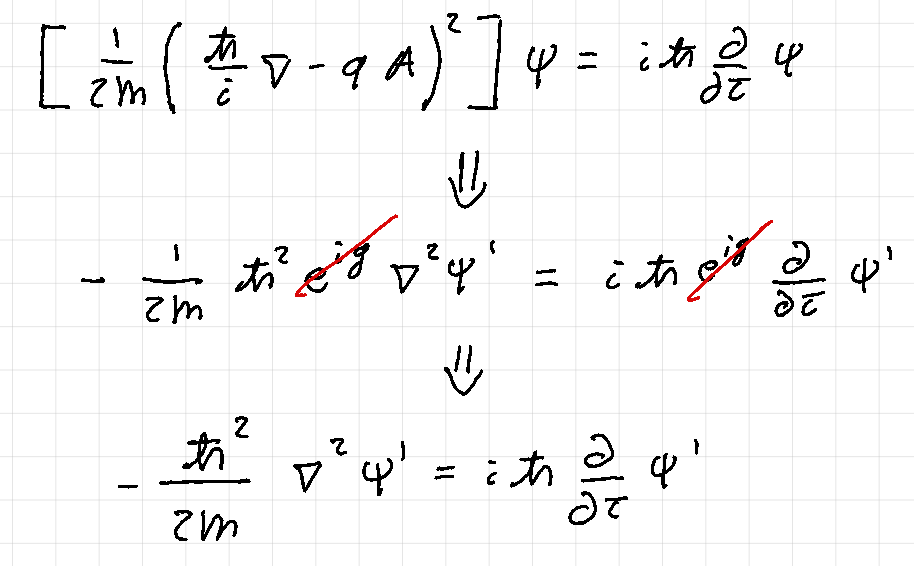
the new equation is the Schrödinger equation of the free particle is much simpler than the previous one.

As we have seen, the effect of is to change the phase of the wave function

We recognize that the total phase of a wave function is given by

1. The Magnetic Vector Potential Contribution: This term represents the phase shift acquired by a charged particle due to the presence of a magnetic vector potential. This integral is evaluated along the path of the particle from an initial point ​ to a final point . This term is responsible for the Aharonov-Bohm effect, where the particle acquires an additional phase in regions where the magnetic field is zero but the vector potential is non-zero.

2. The Initial Phase (): This term represents the initial phase of the wave function at the starting point of the path. It’s essentially the phase the wave function would have in the absence of the vector potential .

Reflected and transmitted waves

We can treat the ring as a barrier problem with propagating, reflected and transmitted waves

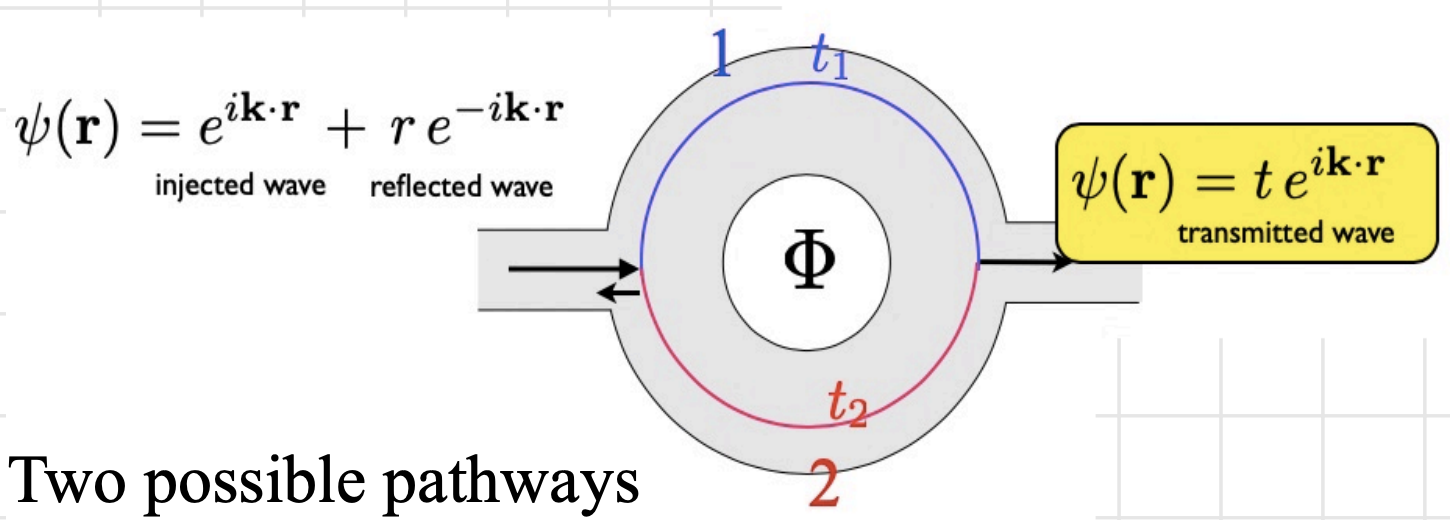
we have incoming waves with an amplitude of , a reflected wave with an amplitude of , and a transmitted wave with an amplitude of . The transmitted amplitudes of the two paths are combined as follows:

It’s important to note that in general, the amplitudes (, ) are complex quantities, and they can be expressed as:

the total transmission probability is given by:

Depending on the path taken, the electron and will be either parallel or antiparallel

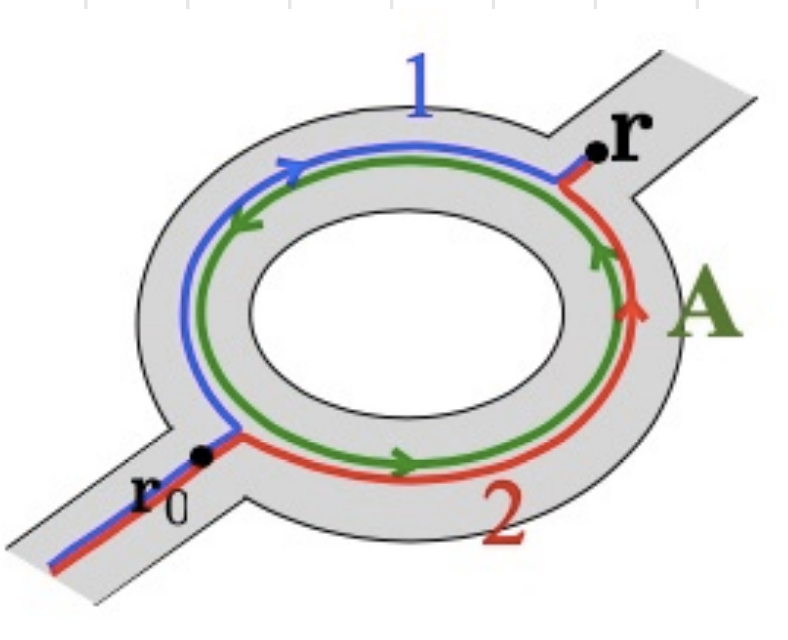
We use the new definition of the phase that includes to find the phase difference between path 1 and 2 from the fixed reference point to a position past the ring

The sign of this term is determined by the sign of the charge of the particle. We notice that the sum of the two paths is the loop integral that we know being equal to the flux:

The sign of the term related to the path 1 is due to the fact that has opposite direction along the two path. Finally the total phase difference between the two paths, taking into account the effect of the vector potential, can be expressed as the difference in the initial phases plus a term dependent on the magnetic flux ​ enclosed by the paths:

The phase difference between the wave functions of electrons taking two different paths around the magnetic flux is a function of the enclosed magnetic flux, even if there is no magnetic field present in the region where the electrons are traveling (because we are outside the solenoid). The interference pattern resulting from the two electron paths can be constructive, destructive, or somewhere in between, depending on the phase difference. The constructive interference amplifies the signal, and the destructive interference diminishes it.

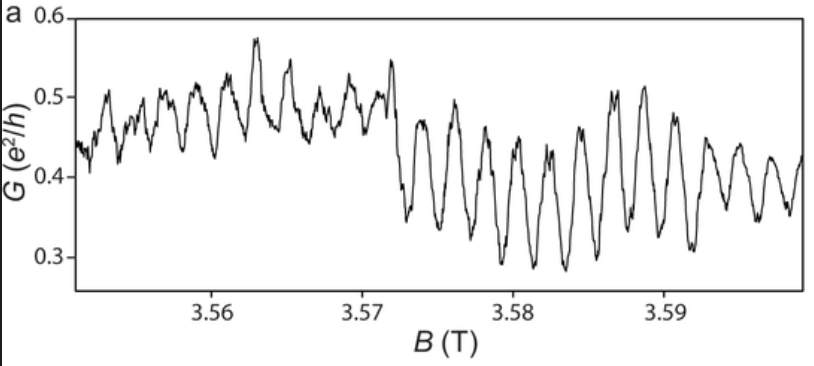
The image shows an oscillatory pattern in the measurement of the conductance () as a function of the magnetic field strength. The oscillations in conductance are a direct result of the phase differences caused by the Aharonov-Bohm effect.