Lorentz model

To study how light interacts with matter we can, as a first approximation, think about a dampened harmonic oscillator that evolves according to the following second order differential equation

where is the displacement of the oscillator with respect to the rest position.

The idea of the Lorentz model is to model the electronic cloud as a mass attached to the nucleus by a spring.

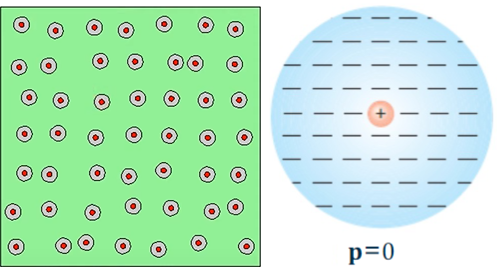
When no external electrostatic field is applied, the distribution of electrons is centered around the nucleus and thus there is no electric dipole moment () as visible in the images below.

As soon as we apply a varying electric field the electron cloud feels a force associated to the field and a restoring force due to the attraction to the nucleus (which has a much bigger mass compared to the one of the electron). We also have a friction force proportional to the velocity of the electrons. In this case we have a net dipole moment due to the fact that the electron cloud is not centered anymore around the nucleus.

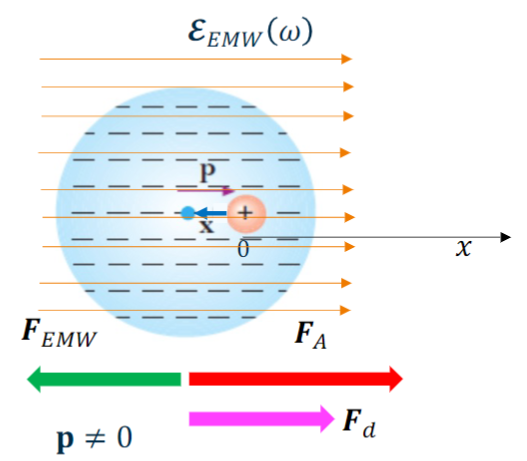
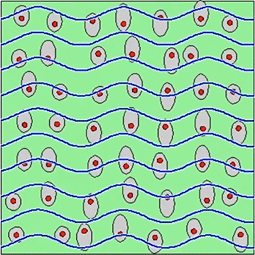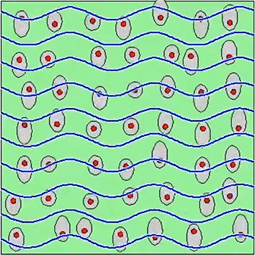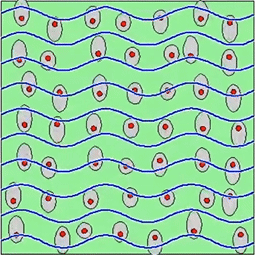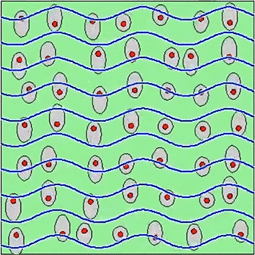
In case of a single electron we can write the following equation to describe its motion around the rest position:

where is the position relative to the rest position (i.e. the nucleus), is the elastic constant of the restoring force and is the damping constant due to dissipation.

The resonant frequency is given by

If we now consider the complex field of a linearly polarized monochromatic plane wave as the product of magnitude and phase we get (using the equation above and the definition of )

whose steady state solutions are given by

The real part of is the displacement of the electron with respect to its rest position.

todo explain better the formula

Complex polarization

Similarly to what was done for the electromagnetic field, we can write the polarization as a complex quantity

In the case of a medium represented by a gas of atoms per unit volume with a single electron each, we can rewrite the complex polarization in the following form

todo why the step after ?

in this case is considered as an average of the electron displacement over the considered volume.

The same expression can be obtained for a generic electron displacement :

We can then extract the real parts from the equation above to get

Frequency dependent optical susceptibility

From we can derive the expression for the frequency dependent optical susceptibility:

with

Plotting the real and imaginary parts of the susceptibility in units of we can see that far from the resonant frequency of the atom the susceptibility is not dependent on the frequency (which is the scenario considered in the first part of the course).

Displacement vector

Recalling the definition of electric displacement:

if we consider the displacement vector as a complex quantity we get

Absorption and dispersion

Source of the animations